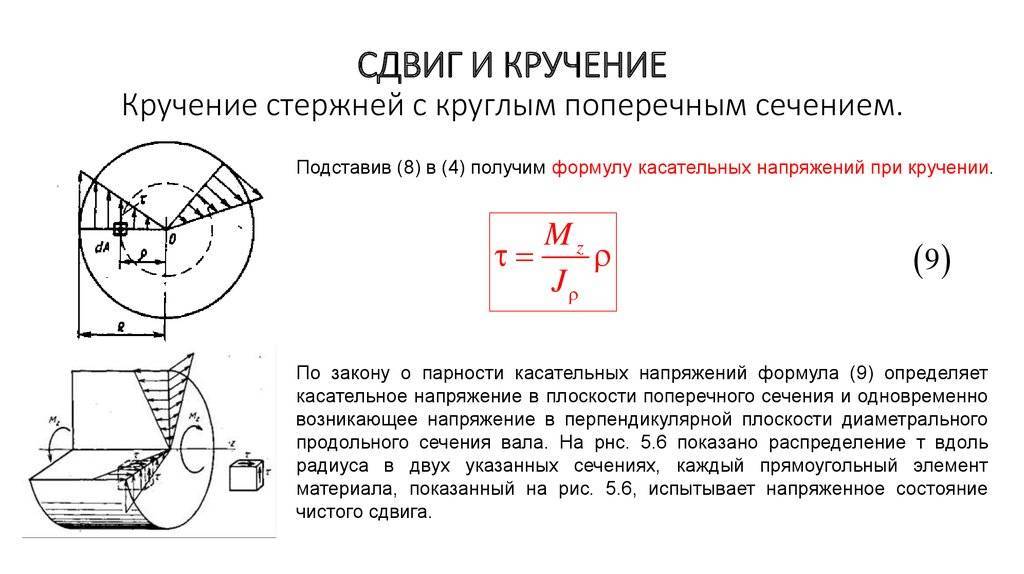
Деформация сдвига

Деформация изгиба

Рассмотрим примеры деформации данного вида. В случае изгиба, выпуклая часть тела подвергается некоторому растяжению, а вогнутый фрагмент сжимается. Внутри тела, подвергающегося данному варианту деформации, есть слой, который не испытывает ни сжатия, ни растяжения. Его принято называть нейтральным участком деформируемого тела. Вблизи него можно уменьшить площадь тела.

В технике примеры деформации данного типа используют для экономии материалов, а также для уменьшения веса возводимых конструкций. Сплошные брусья и стержни заменяют трубами, рельсами, двутавровыми балками.

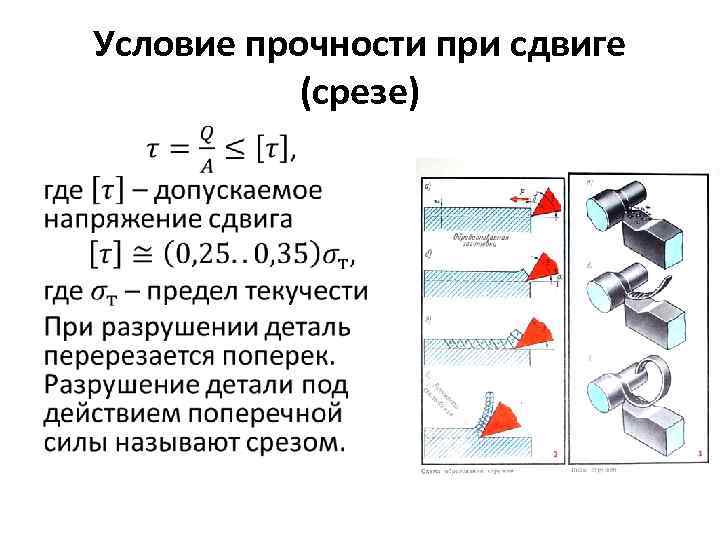
Напряжение при сдвиге

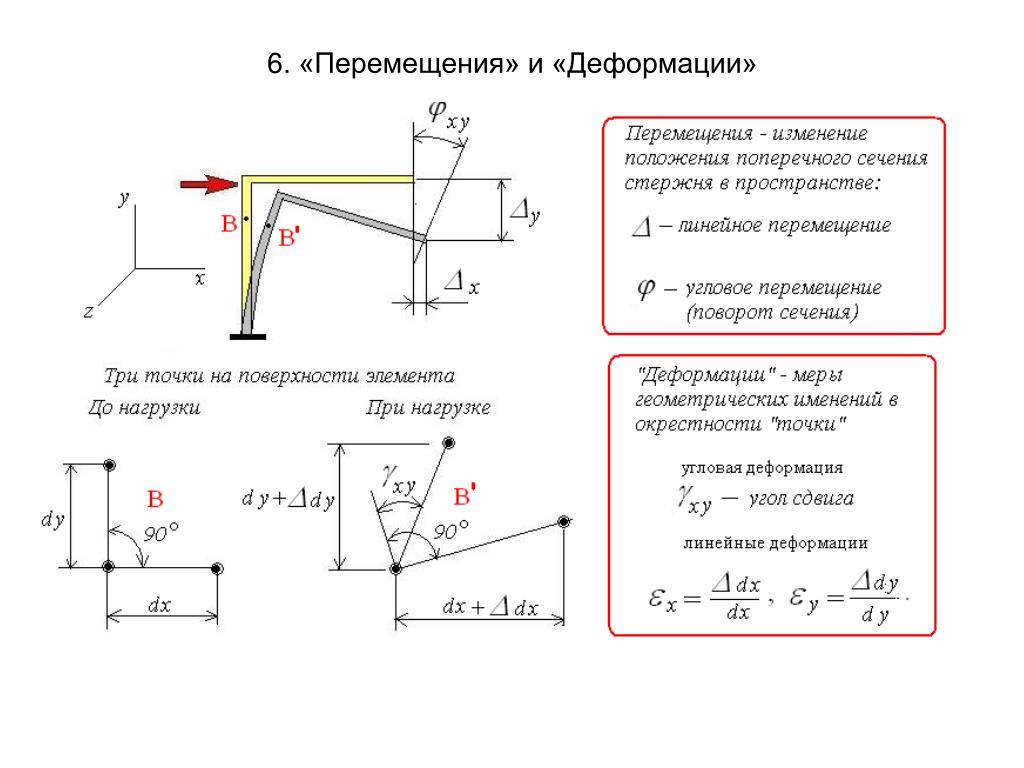
Воздействие внешней силы на грань приводит к возникновению в изделии изменения формы. Все напряжения делятся на две категории: нормальные и касательные. Нормальными считаются внутренние напряжения, возникающие в различных слоях изделия, подверженного деформации.

Напряжения и деформации при сдвиге описываются с применением аналитических выражений и графических изображений. Общее состояние описывается пространственным (трёхкоординатным) напряжением. Если в конкретном случае можно выявить сечения, в которых оба вида напряжений равны нулю, можно перейти к более простым моделям описания этого процесса. Ими являются двухкоординатное (плоское) напряжённое состояние или линейное. Две последних модели являются частными случаями трёхкоординатного напряжённого состояния.

 

Касательные напряжения являются мерой скольжения одного поперечного слоя относительно другого. В изменениях на поверхности каждого слоя возникают только касательные напряжения. Для оценки полной картины деформации используют следующие теоретические положения:

• закон парности касательных напряжений;
• вычисление экстремальных нормальных напряжений;
• определение всех тангенциальных напряжений.

Оценка их всех при деформации смещения позволят оценить прочность конструкции.

Деформация изгиба

Рассмотрим примеры деформации данного вида. В случае изгиба, выпуклая часть тела подвергается некоторому растяжению, а вогнутый фрагмент сжимается. Внутри тела, подвергающегося данному варианту деформации, есть слой, который не испытывает ни сжатия, ни растяжения. Его принято называть нейтральным участком деформируемого тела. Вблизи него можно уменьшить площадь тела.

В технике примеры деформации данного типа используют для экономии материалов, а также для уменьшения веса возводимых конструкций. Сплошные брусья и стержни заменяют трубами, рельсами, двутавровыми балками.

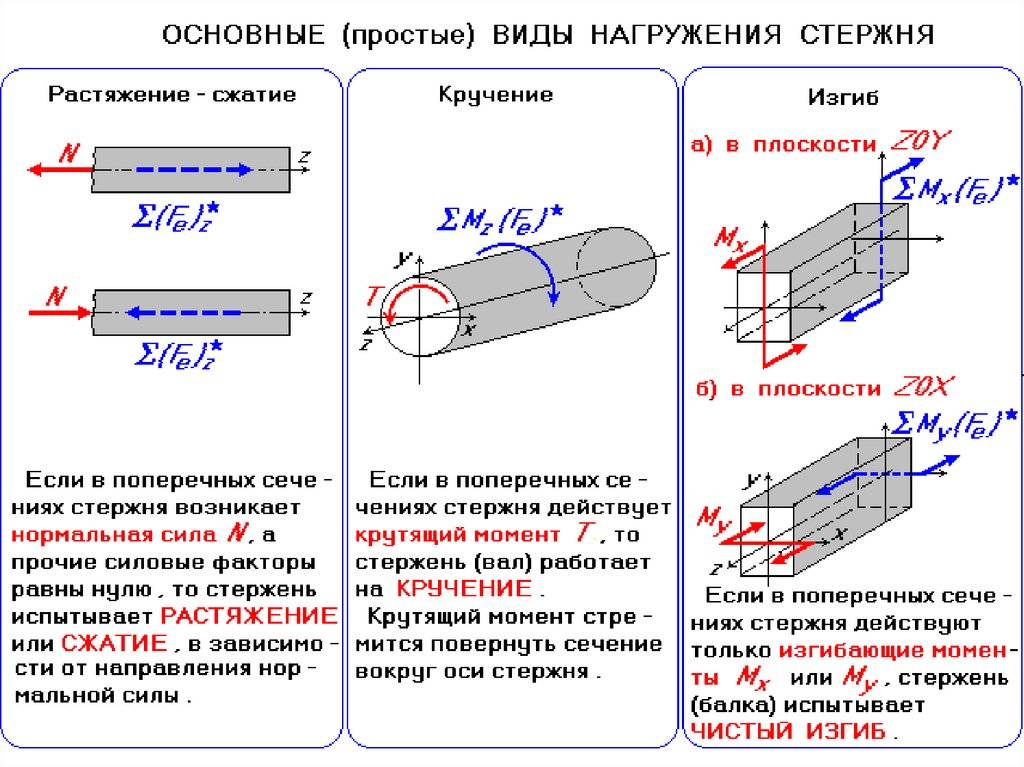
Кручение

Если виды механических деформаций разделяли бы по сложности вычислений, то этот занял бы первое место. Такой вид изменения формы тела возникает при воздействии на него двух сил. При этом смещение любой точки тела происходит перпендикулярно к оси воздействующих сил. Говоря о таком типе деформации, следует упомянуть следующие величины, подлежащие вычислению:

1. Ф — угол закручивания цилиндрического стержня.
2. Т — момент действия.
3. Л — длина стержня.
4. Г — момент инерции.
5. Ж — модуль сдвига.

Формула выглядит так:

Ф=(Т*Л)/(Г*Ж).

Другая величина, требующая вычисления, это относительный угол закручивания:

Q=Ф/Л (значения берутся из предыдущей формулы).

Сжатие и растяжение

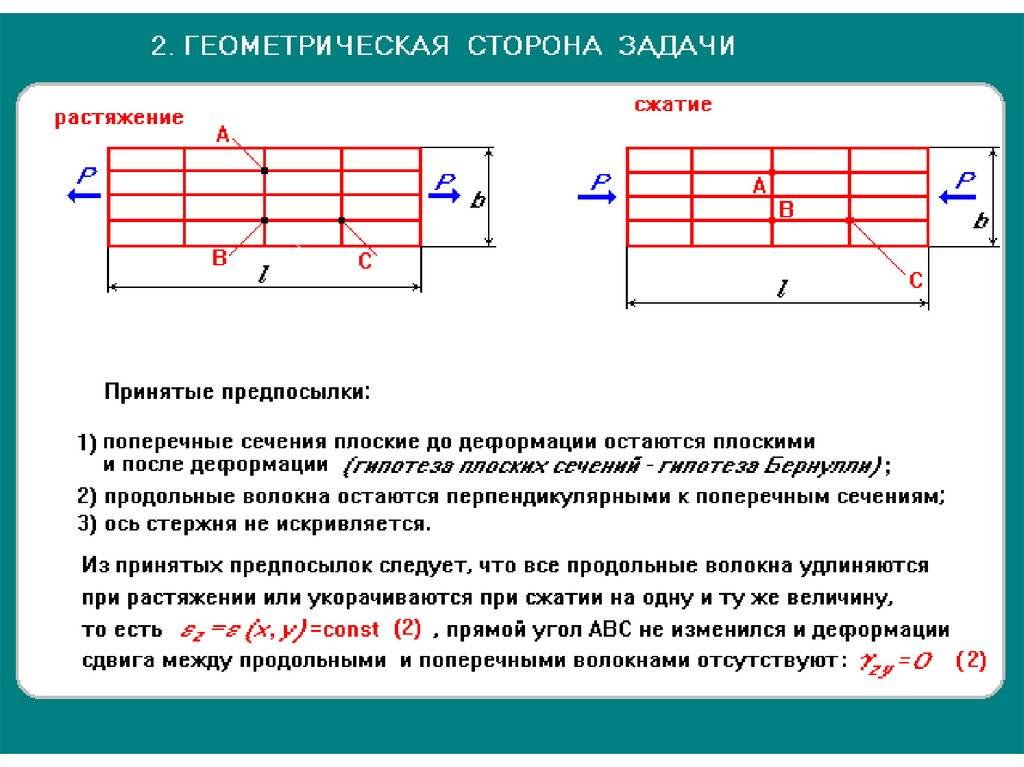
Деформация растяжения связана с относительным либо абсолютным удлинением тела. В качестве примера можно привести однородный стержень, который закреплен с одного конца. При приложении вдоль оси силы, действующей в противоположном направлении, наблюдается растягивание стержня.

Сила же, прикладываемая по направлению к закрепленному концу стержня, приводит к сжатию тела. В процессе сжатия либо растяжения происходит изменение площади сечения тела.

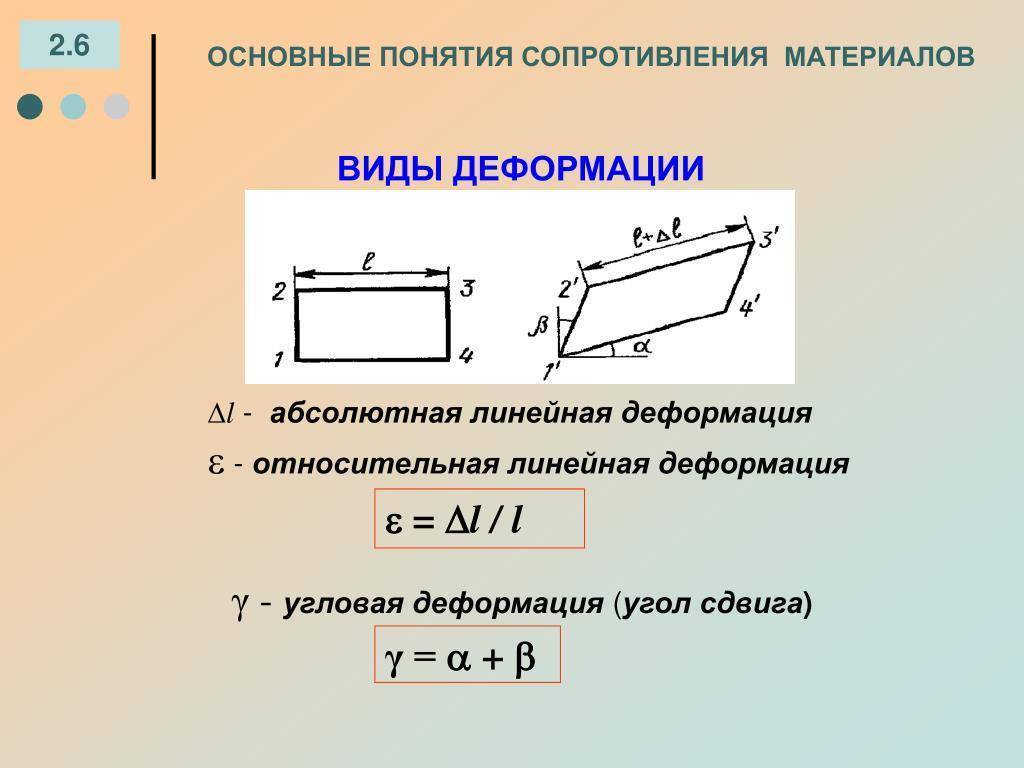
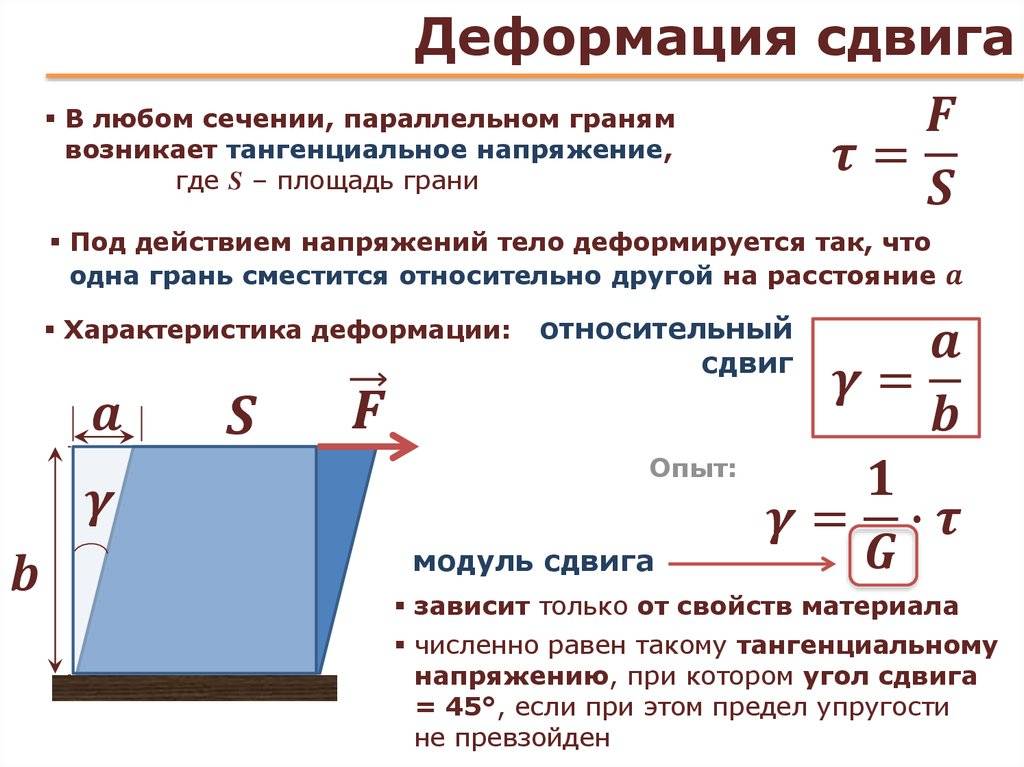
Деформация растяжения – это изменения состояния объекта, сопровождающиеся смещением его слоев. Данный вид можно проанализировать на модели твердого тела, состоящего из параллельных пластин, которые между собой соединены пружинками. За счет горизонтальной силы осуществляется сдвиг пластин на какой-то угол, объем тела при этом не меняется. В случае упругих деформаций между силой, приложенной к телу, и углом сдвига выявлена прямо пропорциональная зависимость.

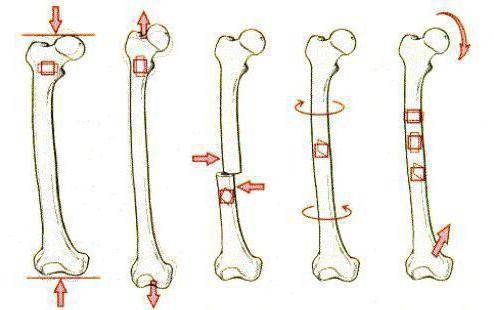
Испытание на вязкость разрушения

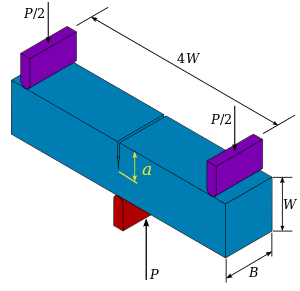Single-кромочные вырезы -bending образца (также называют три точки изгиба образца) для испытания трещиностойкости.

Вязкость разрушения образца также можно определить , используя тест на трехточечный изгиб. Коэффициент интенсивности напряжений в вершине трещины образца изгиба с одиночным надрезом равен

Kязнак равно4пBπW1.6(аW)12-2,6(аW)32+12,3(аW)52-21,2(аW)72+21,8(аW)92{\ displaystyle {\ begin {align} K _ {\ rm {I}} & = {\ frac {4P} {B}} {\ sqrt {\ frac {\ pi} {W}}} \ left [1.6 \ left ({\ frac {a} {W}} \ right) ^ {1/2} -2,6 \ left ({\ frac {a} {W}} \ right) ^ {3/2} +12,3 \ left ({ \ frac {a} {W}} \ right) ^ {5/2} \ right. \\ & \ qquad \ left.-21.2 \ left ({\ frac {a} {W}} \ right) ^ {7 /2}+21,8\left({\frac {a} {W}} \ right) ^ {9/2} \ right] \ end {align}}}

где – приложенная нагрузка, – толщина образца, – длина трещины, – ширина образца. При испытании на трехточечный изгиб усталостная трещина создается на вершине надреза в результате циклического нагружения. Измеряется длина трещины. Затем образец загружается монотонно. График зависимости нагрузки от смещения раскрытия трещины используется для определения нагрузки, при которой трещина начинает расти. Эта нагрузка подставляется в приведенную выше формулу для определения вязкости разрушения . п{\ displaystyle P}B{\ displaystyle B}а{\ displaystyle a}W{\ displaystyle W}Kяc{\ displaystyle K_ {Ic}}

Стандарты ASTM D5045-14 и E1290-08 предлагают соотношение

Kязнак равно6пBWа12Y{\ displaystyle K _ {\ rm {I}} = {\ cfrac {6P} {BW}} \, a ^ {1/2} \, Y}

где

Yзнак равно1,99-аW(1-аW)(2,15-3,93аW+2,7(аW)2)(1+2аW)(1-аW)32.{\ displaystyle Y = {\ cfrac {1,99-a / W \, (1-a / W) (2,15–3,93a / W + 2,7 (а / W) ^ {2})} {(1 + 2a / W ) (1-а / W) ^ {3/2}}} \ ,.}

Прогнозируемые значения практически идентичны для уравнений ASTM и Бауэра для длин трещин менее 0,6 . Kя{\ displaystyle K _ {\ rm {I}}}W{\ displaystyle W}

Примечания и ссылки

1. ↑ и Эуг Роффиан, Теоретический и практический трактат о сопротивлении материалов в конструкциях , Феликс Удар, 1858 г.
2. Ландау Л.Д., Липшиц Е.М., Теория упругости , 3- е  изд. , 1970, 1-172.
3. LRG Treloar , The Physics of Rubber Elasticity , Oxford, Clarendon Press,1975 г., 310  с. ( ISBN  978-0-19-851355-1 ) , стр.  2.
4. ↑ и Gijsbertus de With , Структура, деформация и целостность материалов, том I: Основы и эластичность , Weinheim, Wiley VCH,2006 г., 838  с. ( ISBN  978-3-527-31426-3 ) , стр.  32.
5. Понятие модуля сжимаемости неоднозначно, поскольку оно является обратным так называемой «сжимаемости».
6. Уравнение идеального газа дает χ _T = 1 / P , или K = P = 10 5  Па = 10 -4  ГПа при 1  атм .

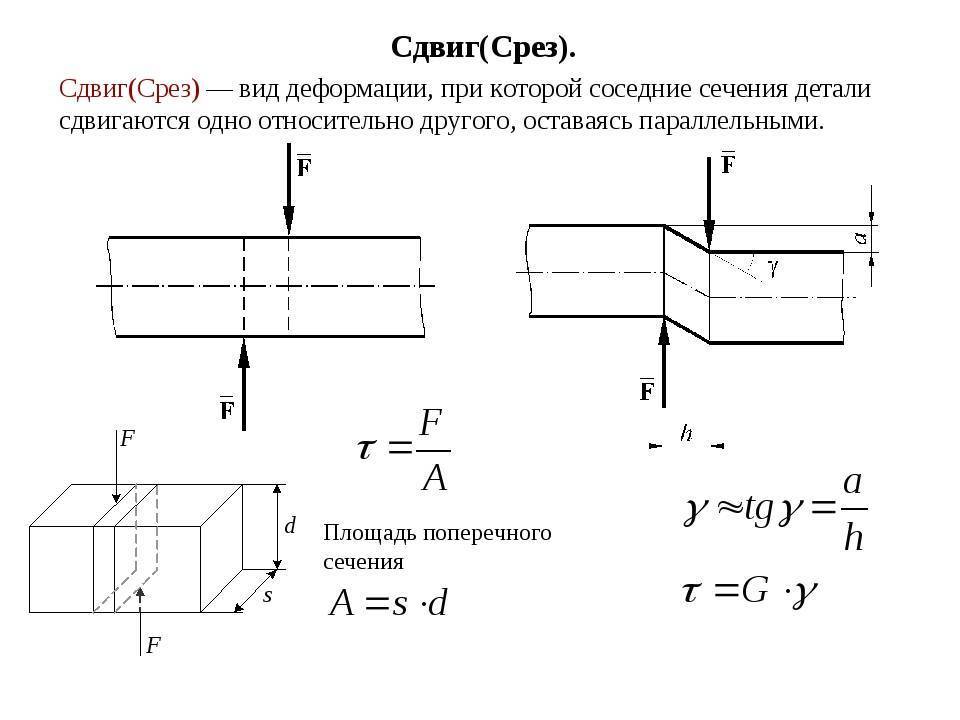
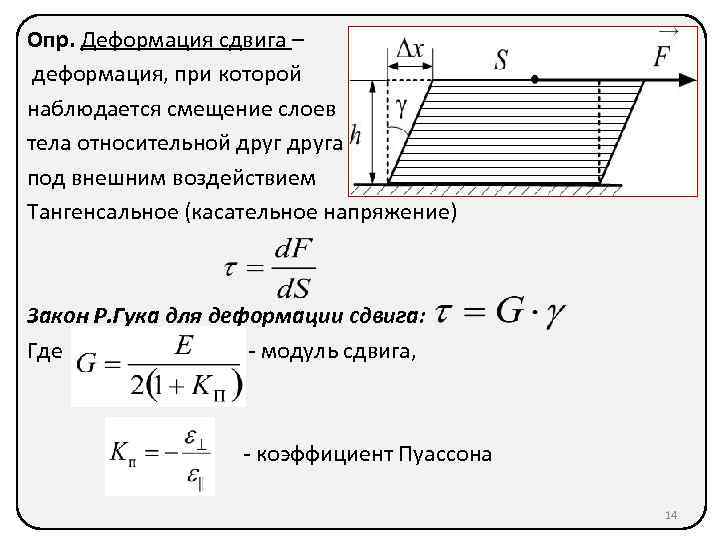
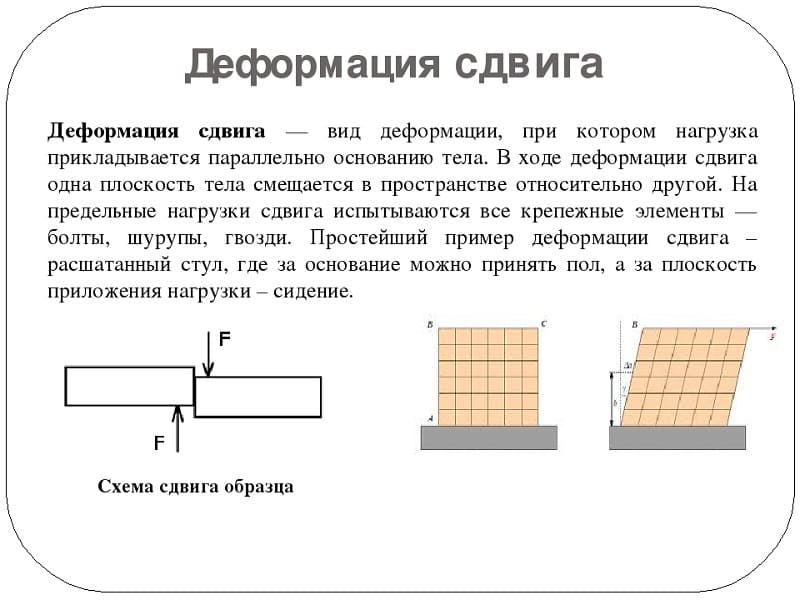
Определение и общие сведения о деформации сдвига

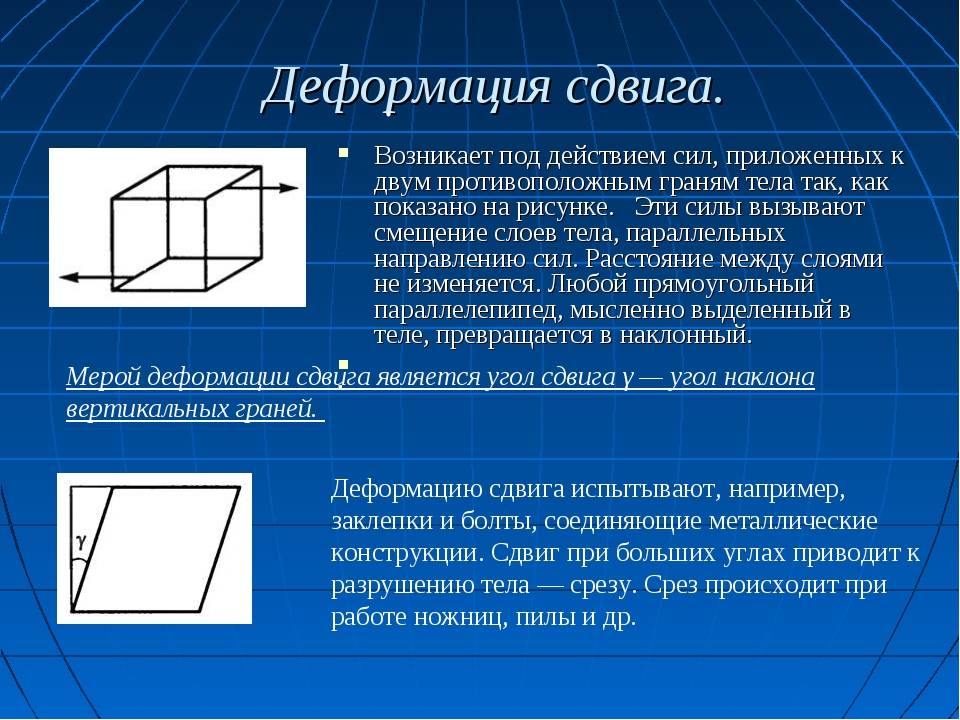
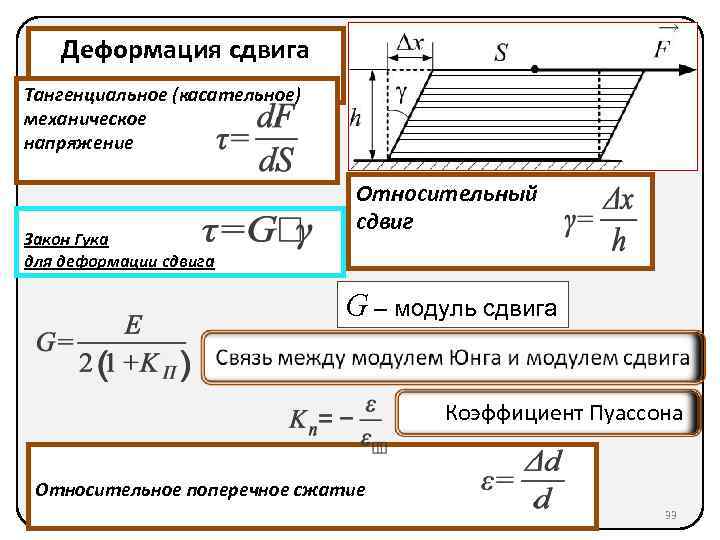
Основным признаком, характеризующим деформацию сдвига, является сохранение постоянства объёма. Не зависимо от того, в каком направлении действуют силовые факторы этот параметр остаётся неизменным.

Примеры проявления деформации сдвига можно обнаружить при проведении различного рода работ. К таким случаям относятся:

• при распиловке бруса;
• отрезание или рубка металла;
• в результате нарушения целостности крепления металлических или деревянных деталей, соединённых метизами;
• балки в местах крепления опор;
• места скрепления мостовых пролётов;
• крепёж на перемычках соединения железнодорожных рельс;
• разрезания листа бумаги ножницами.

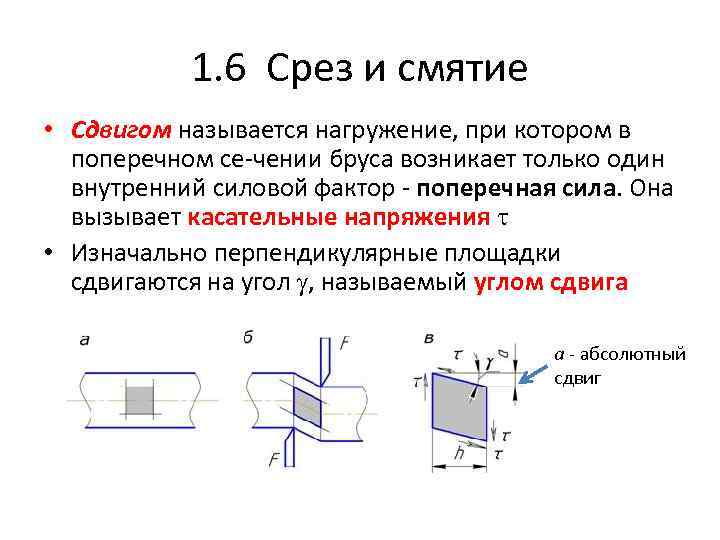
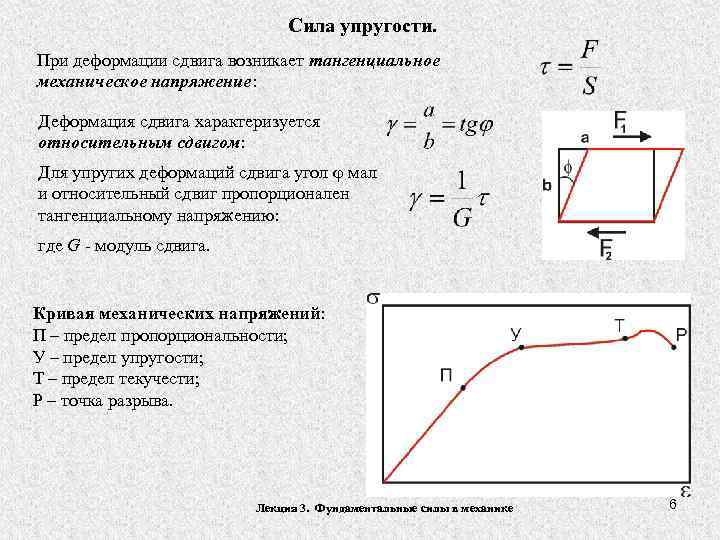
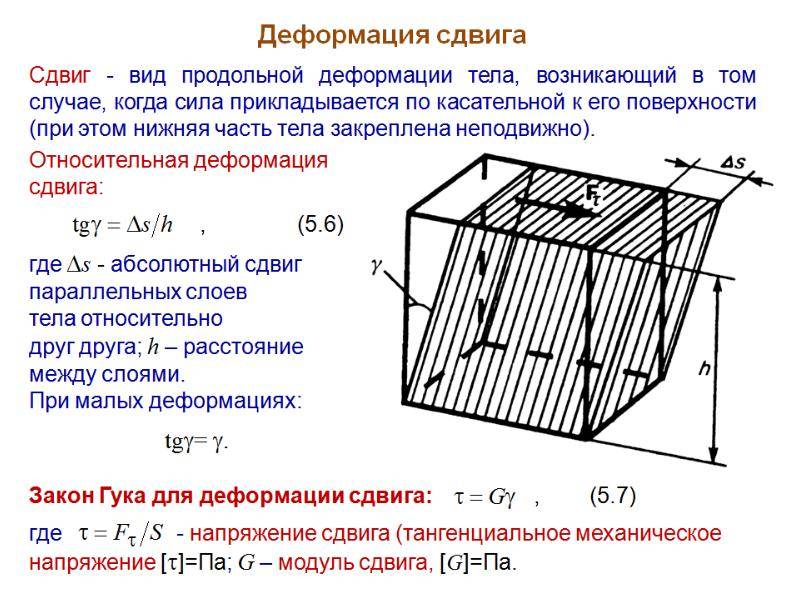
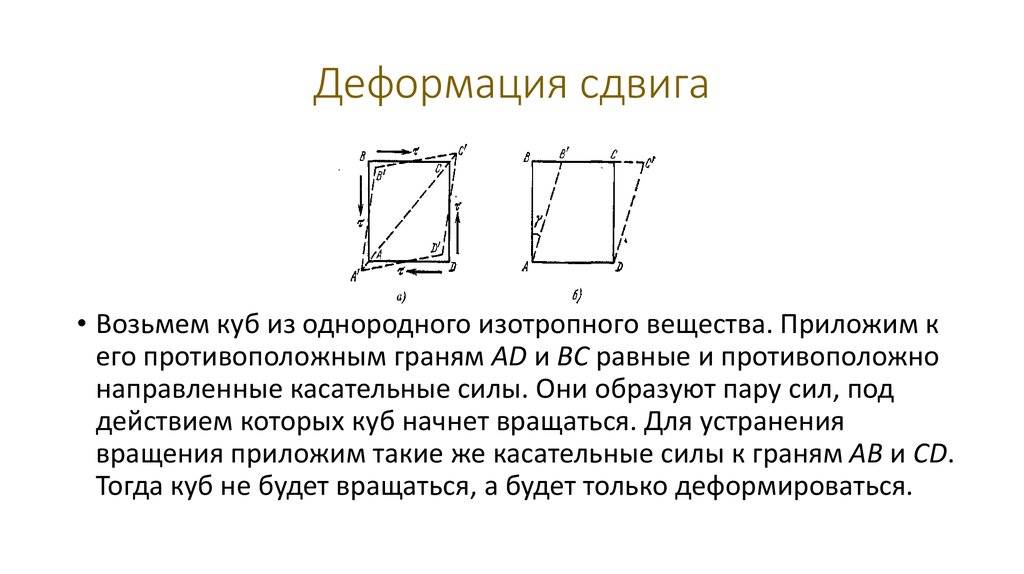
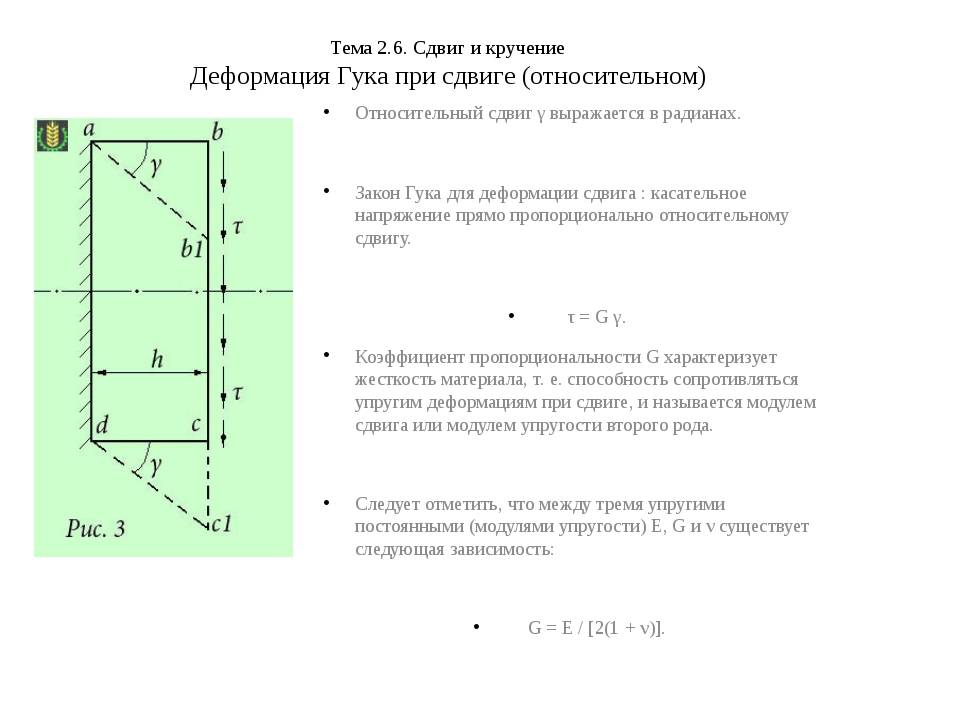
При определённых условиях наблюдается чистый сдвиг. Он определяется как сдвиг, при котором на все четыре грани (например, прямоугольной детали) оказывают воздействие только напряжения, направленные по касательной к поверхности. В этом случае произойдёт плавный сдвиг всех слоёв детали от верхних к нижним слоям. Тогда внешняя сила изменяет форму детали, а объём сохраняется.

Для оценки величины сдвига и надёжности конструкции используют следующие параметры:

• величина, направление и точка приложения воздействующей силы;
• модуль сдвига;
• угол изменения внешних граней изделия;
• тангенциальное напряжение;
• модуль кручения (зависит от физико-механических характеристик материала);

Расчёт и практическое измерение этих параметров необходимы для оценки устойчивости и целостности конструкции. Формула, позволяющая вычислить допустимые изменения, учитывает все воздействия на конкретные слои детали и всю конструкции в целом.

В случае воздействия деформации величина угла считается пропорциональной внешней силе. Увеличение степени воздействия может превратить деформацию сдвига в срез. Это приведёт к разрушению не только элементов крепления (болтов, шпилек, заклёпок), но и всей детали.

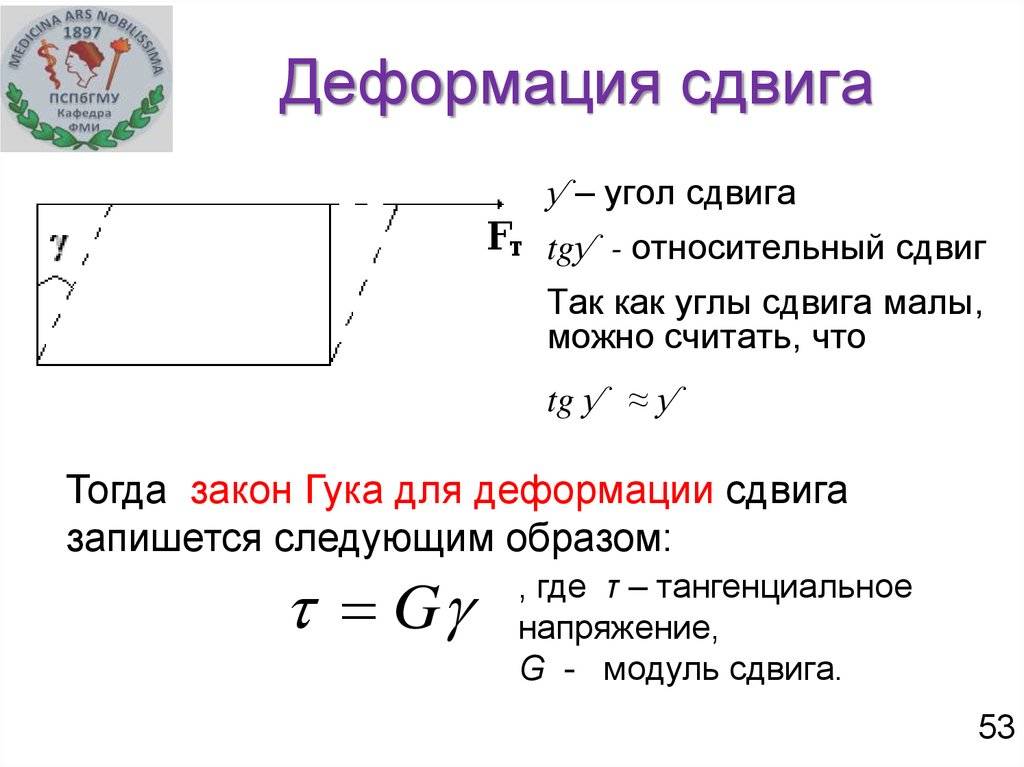
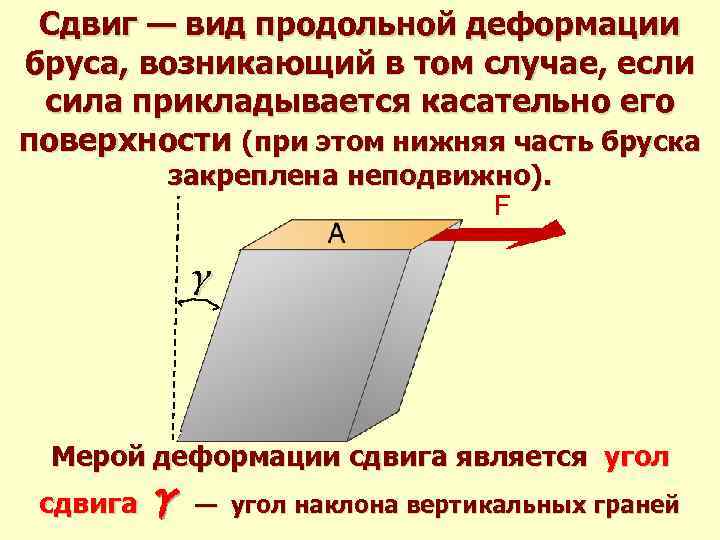
Для наглядности изменения формы детали при деформации сдвига динамика процесса обозначается с помощью величины угла смещения и векторов возникающих напряжений. Действующая сила направлена в сторону смещения слоёв рассматриваемой детали.

В современных условиях угол сдвига измеряется различными техническими приборами. Основным прибором для измерения параметров смещения является тензомер. Эти приборы работают на различных физических принципах:

• оптические (в том числе лазерные);
• акустические;
• рентгеновские; электрические;
• пневматические.

В этих приборах относительная деформация сдвига обрабатывается на современных вычислительных средствах с применением соответствующего программного обеспечения. Каждый метод обладает своими достоинствами и недостатками. Их применение зависит от поставленной задачи, технической и финансовой возможности.

Определение и общие сведения о деформации сдвига

Основным признаком, характеризующим деформацию сдвига, является сохранение постоянства объёма. Не зависимо от того, в каком направлении действуют силовые факторы этот параметр остаётся неизменным.

Примеры проявления деформации сдвига можно обнаружить при проведении различного рода работ. К таким случаям относятся:

• при распиловке бруса;
• отрезание или рубка металла;
• в результате нарушения целостности крепления металлических или деревянных деталей, соединённых метизами;
• балки в местах крепления опор;
• места скрепления мостовых пролётов;
• крепёж на перемычках соединения железнодорожных рельс;
• разрезания листа бумаги ножницами.

При определённых условиях наблюдается чистый сдвиг. Он определяется как сдвиг, при котором на все четыре грани (например, прямоугольной детали) оказывают воздействие только напряжения, направленные по касательной к поверхности. В этом случае произойдёт плавный сдвиг всех слоёв детали от верхних к нижним слоям. Тогда внешняя сила изменяет форму детали, а объём сохраняется.

Для оценки величины сдвига и надёжности конструкции используют следующие параметры:

• величина, направление и точка приложения воздействующей силы;
• модуль сдвига;
• угол изменения внешних граней изделия;
• тангенциальное напряжение;
• модуль кручения (зависит от физико-механических характеристик материала);

Расчёт и практическое измерение этих параметров необходимы для оценки устойчивости и целостности конструкции. Формула, позволяющая вычислить допустимые изменения, учитывает все воздействия на конкретные слои детали и всю конструкции в целом.

В случае воздействия деформации величина угла считается пропорциональной внешней силе. Увеличение степени воздействия может превратить деформацию сдвига в срез. Это приведёт к разрушению не только элементов крепления (болтов, шпилек, заклёпок), но и всей детали.

Для наглядности изменения формы детали при деформации сдвига динамика процесса обозначается с помощью величины угла смещения и векторов возникающих напряжений. Действующая сила направлена в сторону смещения слоёв рассматриваемой детали.

В современных условиях угол сдвига измеряется различными техническими приборами. Основным прибором для измерения параметров смещения является тензомер. Эти приборы работают на различных физических принципах:

• оптические (в том числе лазерные);
• акустические;
• рентгеновские; электрические;
• пневматические.

В этих приборах относительная деформация сдвига обрабатывается на современных вычислительных средствах с применением соответствующего программного обеспечения. Каждый метод обладает своими достоинствами и недостатками. Их применение зависит от поставленной задачи, технической и финансовой возможности.

Этапы мониторинга и наблюдения за деформацией зданий и сооружений

Этапы

Первый этап
Собирают и изучают техническую документацию, сведения по строительству и эксплуатации объекта.Составляют рабочую программу, где отмечают цель и задачи измерений, намечают расположение геодезических знаков, составляют график работ и выбирают метод измерений.

Второй этап
Включает осмотр и обследование территории и надземных конструкций сооружения, здания

Особое внимание специалисты уделяют близлежащим постройкам и устройствам для отвода поверхностных вод.Проектируют, изготавливают и устанавливают геодезические знаки, проводят измерения по графику в соответствии с выбранной методикой.
Осматривают внешнее состояние здания, конструкций, делают замеры с помощью оборудования и собирают образцы для установления прочности, плотности, водопроницаемости и другие необходимые физико-механические характеристики. Третий этап
Обследуют фундаменты и грунты в основании объекта

Закладывают шурфы в аварийной зоне и за её пределами, а потом сравнивают результаты

Третий этап
Обследуют фундаменты и грунты в основании объекта. Закладывают шурфы в аварийной зоне и за её пределами, а потом сравнивают результаты

Во время реконструкции проводят обследование всех колонн и стен. Делают поверку полевых журналов, оценивают точность проведённых полевых работ. Составляют ведомости по каждому циклу. Составляют отчёты по результатам и оформляют их графически.

Геодезический контроль за деформациями заключается в том, чтобы периодически проверять положение точек сооружений, обозначенных марками, относительно неподвижных знаков по вертикали и горизонтали. Замеры и вычисления проводятся дистанционно бесконтактным способом. Так, с помощью тахеометра устанавливаются пространственные координаты критичных точек, а результаты выполняются автоматически и высвечиваются на экране дисплея. Осадки определяются с помощью высокоточного нивелира.

Сжатие и растяжение

Деформация растяжения связана с относительным либо абсолютным удлинением тела. В качестве примера можно привести однородный стержень, который закреплен с одного конца. При приложении вдоль оси силы, действующей в противоположном направлении, наблюдается растягивание стержня.

Сила же, прикладываемая по направлению к закрепленному концу стержня, приводит к сжатию тела. В процессе сжатия либо растяжения происходит изменение площади сечения тела.

Деформация растяжения – это изменения состояния объекта, сопровождающиеся смещением его слоев. Данный вид можно проанализировать на модели твердого тела, состоящего из параллельных пластин, которые между собой соединены пружинками. За счет горизонтальной силы осуществляется сдвиг пластин на какой-то угол, объем тела при этом не меняется. В случае упругих деформаций между силой, приложенной к телу, и углом сдвига выявлена прямо пропорциональная зависимость.

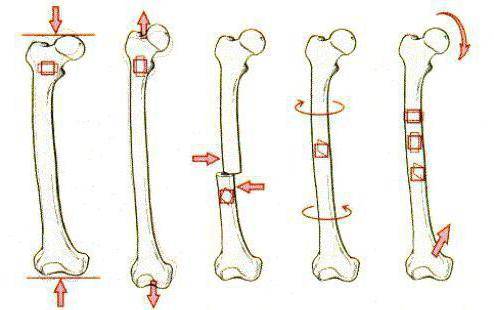
Кручение

Если виды механических деформаций разделяли бы по сложности вычислений, то этот занял бы первое место. Такой вид изменения формы тела возникает при воздействии на него двух сил. При этом смещение любой точки тела происходит перпендикулярно к оси воздействующих сил. Говоря о таком типе деформации, следует упомянуть следующие величины, подлежащие вычислению:

1. Ф — угол закручивания цилиндрического стержня.
2. Т — момент действия.
3. Л — длина стержня.
4. Г — момент инерции.
5. Ж — модуль сдвига.

Формула выглядит так:

Ф=(Т*Л)/(Г*Ж).

Другая величина, требующая вычисления, это относительный угол закручивания:

Q=Ф/Л (значения берутся из предыдущей формулы).

Примеры деформаций

Однородные (или аффинные) деформации полезны для выяснения поведения материалов. Представляют интерес некоторые однородные деформации.

• равномерное расширение
• чистое расширение
• равноосное растяжение
• простой сдвиг
• чистый сдвиг

Плоские деформации также представляют интерес, особенно в экспериментальном контексте.

Плоская деформация

Плоская деформация, также называемая плоская деформация, это тот, где деформация ограничивается одной из плоскостей в эталонной конфигурации. Если деформация ограничивается плоскостью, описываемой базисными векторами е₁, е₂, то градиент деформации имеет форму

F=F11е1⊗е1+F12е1⊗е2+F21е2⊗е1+F22е2⊗е2+е3⊗е3{ displaystyle { boldsymbol {F}} = F_ {11} mathbf {e} _ {1} otimes mathbf {e} _ {1} + F_ {12} mathbf {e} _ {1} otimes mathbf {e} _ {2} + F_ {21} mathbf {e} _ {2} otimes mathbf {e} _ {1} + F_ {22} mathbf {e} _ {2} otimes mathbf {e} _ {2} + mathbf {e} _ {3} otimes mathbf {e} _ {3}}

В матричной форме

F=F11F12F21F221{ displaystyle { boldsymbol {F}} = { begin {bmatrix} F_ {11} & F_ {12} & 0 F_ {21} & F_ {22} & 0 0 & 0 & 1 end {bmatrix}}}

От теорема о полярном разложении, градиент деформации с точностью до изменения координат можно разложить на растяжение и поворот. Поскольку вся деформация происходит в плоскости, мы можем написать

F=р⋅U=потому что⁡θгрех⁡θ−грех⁡θпотому что⁡θ1λ1λ21{ displaystyle { boldsymbol {F}} = { boldsymbol {R}} cdot { boldsymbol {U}} = { begin {bmatrix} cos theta & sin theta & 0 – sin theta & cos theta & 0 0 & 0 & 1 end {bmatrix}} { begin {bmatrix} lambda _ {1} & 0 & 0 0 & lambda _ {2} & 0 0 & 0 & 1 end {bmatrix}}}

куда θ угол поворота и λ₁, λ₂ являются основные участки.

Изохорная плоская деформация

Если деформация изохорная (с сохранением объема), то det (F) = 1 и у нас есть

F11F22−F12F21=1{ displaystyle F_ {11} F_ {22} -F_ {12} F_ {21} = 1}

В качестве альтернативы,

λ1λ2=1{ displaystyle lambda _ {1} lambda _ {2} = 1}

Простой сдвиг

А простой сдвиг Деформация определяется как деформация изохорной плоскости, в которой имеется набор линейных элементов с заданной базовой ориентацией, которые не изменяют длину и ориентацию во время деформации.

Если е₁ фиксированная исходная ориентация, при которой линейные элементы не деформируются во время деформации, тогда λ₁ = 1 и F·е₁ = е₁.Следовательно,

F11е1+F21е2=е1⟹F11=1 ;  F21={ displaystyle F_ {11} mathbf {e} _ {1} + F_ {21} mathbf {e} _ {2} = mathbf {e} _ {1} quad implies quad F_ {11} = 1 ~; ~~ F_ {21} = 0}

Поскольку деформация изохорная,

F11F22−F12F21=1⟹F22=1{ Displaystyle F_ {11} F_ {22} -F_ {12} F_ {21} = 1 quad подразумевает quad F_ {22} = 1}

Определять

γ:=F12{ displaystyle gamma: = F_ {12} ,}

Тогда градиент деформации при простом сдвиге можно выразить как

F=1γ11{ displaystyle { boldsymbol {F}} = { begin {bmatrix} 1 & gamma & 0 0 & 1 & 0 0 & 0 & 1 end {bmatrix}}}

Сейчас же,

F⋅е2=F12е1+F22е2=γе1+е2⟹F⋅(е2⊗е2)=γе1⊗е2+е2⊗е2{ displaystyle { boldsymbol {F}} cdot mathbf {e} _ {2} = F_ {12} mathbf {e} _ {1} + F_ {22} mathbf {e} _ {2} = gamma mathbf {e} _ {1} + mathbf {e} _ {2} quad подразумевает quad { boldsymbol {F}} cdot ( mathbf {e} _ {2} otimes mathbf {e} _ {2}) = gamma mathbf {e} _ {1} otimes mathbf {e} _ {2} + mathbf {e} _ {2} otimes mathbf {e} _ { 2}}

С

ея⊗ея=1{ displaystyle mathbf {e} _ {i} otimes mathbf {e} _ {i} = { boldsymbol { mathit {1}}}}

мы также можем записать градиент деформации как

F=1+γе1⊗е2{ displaystyle { boldsymbol {F}} = { boldsymbol { mathit {1}}} + gamma mathbf {e} _ {1} otimes mathbf {e} _ {2}}

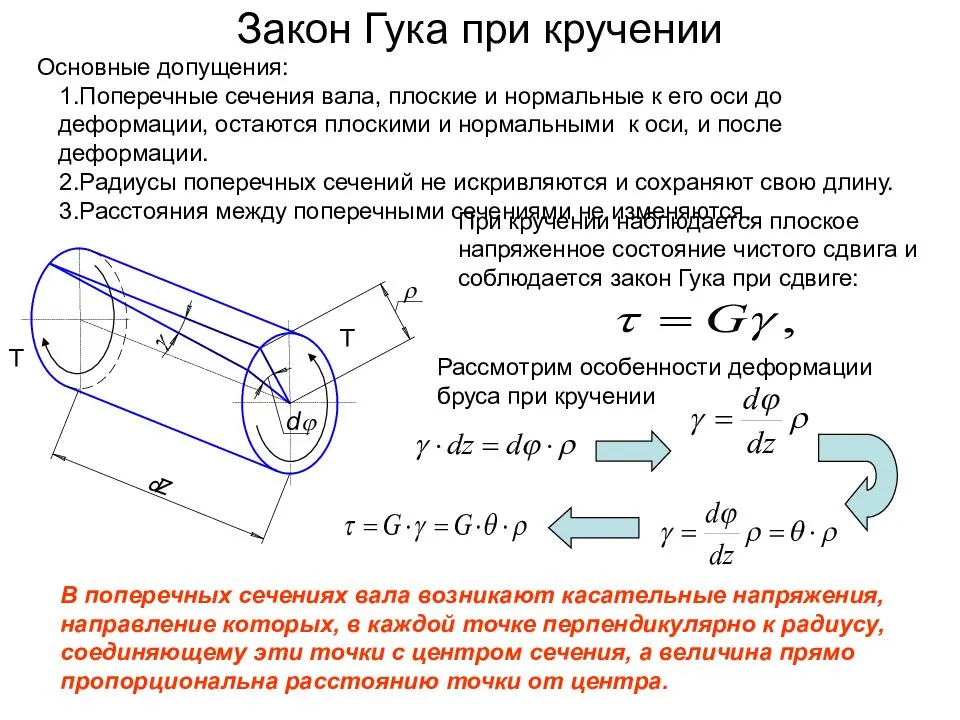
Напряжения кручения

Исходя из приведенного выше определения деформации кручения, при данном процессе в поперечном сечении наблюдаются лишь касательные напряжения, направленные перпендикулярно к радиусам. Их определяют для конкретной точки как произведение соотношения крутящего момента к геометрическому полярному инерционному моменту и расстояния данной точки от оси кручения.

Изменение касательных напряжения линейно, и максимальной величины они достигают на поверхности при наибольших значениях крутящего момента и расстояния от оси кручения, поэтому ее значение вычисляют как частное наибольшего крутящего и полярного моментов сопротивления.

С применением данного условия возможно вычислить прочие параметры: по силовым факторам, создающим крутящий момент – показатель сопротивления и далее размеры сечения в зависимости от формы, либо по размеру сечения – максимально допустимое для него значение крутящего момента и на основе последней допустимые значения внешних нагрузок.

Касательные напряжения, по закону парности, формируются при кручении как в поперечных, так и в продольном направлениях. Вследствие этого во всех точках вала наблюдается деформация в виде чистого сдвига. Главные напряжения направлены к образующей под углом 45°.

Помимо скручивающих усилий возможно воздействие на вал моментной нагрузки.

Из изложенных выше данных следует, что удаление материала в районе оси вала незначительно сказывается на прочности ввиду того, что данная часть мало нагружена. При равных площади сечения и массе деталей кольцевые варианты характеризуются большими полярными моментами сопротивления и инерции по сравнению со сплошными валами. То есть при равной массе полые варианты прочнее и жестче, а при одинаковых показателях прочности и жесткости легче. Названные параметры определяют устойчивость данных изделий к деформации.

Выше были рассмотрены особенности деформации кручения круглых в поперечном разрезе предметов. Для треугольных, прямоугольных, эллиптических и прочих вариантов не применима гипотеза плоских сечений. Это обусловлено тем, что поверхности данного типа при кручении искривляются. Данный процесс их коробления вследствие смещения отдельных точек при деформации вдоль оси называют депланацией. Вследствие этого методы сопротивления материалов для вычисления кручений и напряжений неприменимы. Вместо них используют методы теории упругости.

Для изделий произвольной поперечной формы касательные напряжения имеют направление по касательной к контуру, однако при наличии внешних углов они отсутствуют. Так, при разложении напряжения вблизи угла по нормалям к его сторонам надвое из закона парности следует формирование касательных напряжений на свободной поверхности. Однако в данном случае она свободна от нагрузки, поэтому у внешнего угла касательные напряжения обнуляются.

Для наиболее распространенных среди вариантов некруглого сечения прямоугольных валов наибольшие напряжения характерны для поверхностных участков в середине длинных сторон. Следовательно, там наблюдается наибольшая деформация кручения.

Прямоугольные детали в сравнении с круглым характеризуются значительно меньшими жесткостью и прочностью. Причем это отличие увеличивается с ростом отношения сторон. Следовательно, они более подвержены деформации.

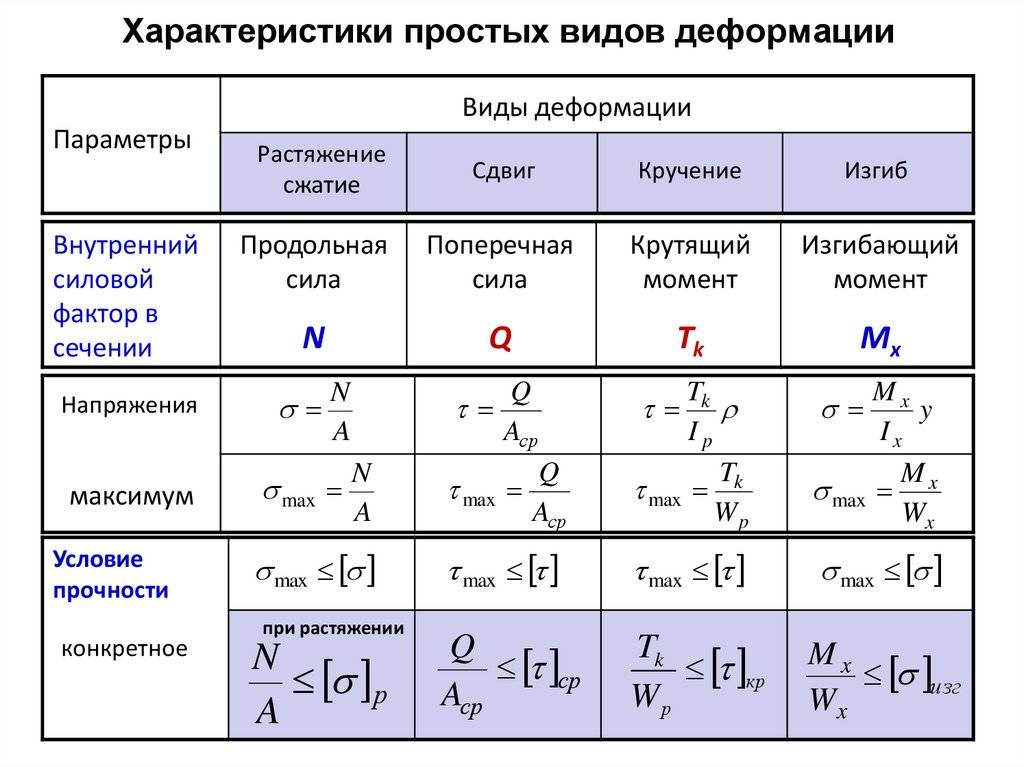
Расчёты на крепость при сдвиге

Оценка характеристик прочности изделий выполняется для определения наступления трёх факторов деформации:

1. Смещение некоторых слоёв (возникновения угла деформации).
2. Смятие крепежных элементов.
3. Сдвиг.
4. Разрыв.

Расчёт на крепость нужен для определения условий наступления любого из видов. В работе для более наглядной оценки параметров прочности и стойкости к деформированию решают существующие аналитические выражения и изображают эпюры отражающие направления влияния разных видов стрессов.

Получение численных параметров возможно благодаря использованию разработанных методов решения систем дифференциальных уравнений. Уточнение аналитических выражений изготавливается на основе принятых гипотез.

Расчёт возможных стрессов изготавливается на основании первой, третьей и четвёртой гипотезы прочности. Любая из гипотез принимается для различных материалов, которые обладают собственными физико-механическими свойствами.

Крепость быть на каждом из этапов разработки определенной детали. В первую очередь вычисляют величины возможных стрессов и угол отклонения на предварительном (проверочном) шаге. Это дает возможность определить их уровни, величины и направление приложенных сил. После чего приступают к проектированию. На данном шаге выполняется подбор материала детали и элементов крепежа с учитыванием достаточной прочности любого элемента конструкции. На конечном шаге ещё один раз проверяют возможные нормы нагрузки и способность готовой детали держать допустимую и дополнительную нагрузку, другими словами формируют прочностный запас.

Наиболее показательными являются расчёты для чистого сдвига. В данном случае при расчёте рассматривают следующие моменты выполнения задачи:

• Статический (составляется уравнение равновесия). В данном случае применяется предположение о равномерности распределения касательных стрессов. Впрочем в определенных случаях они делятся не одинаково, что затрудняет решение установленной задачи. Он дает возможность установить связь возникших стрессов с действующими внешними силами. Это выполняться благодаря получению семейства решений дифференциальных уравнений равновесия для всего объёма детали.
• Геометрический (деформационный). Позволяет отобразить связь между отдельными маленькими участками исследуемой детали.
• Математический. Дает возможность подобрать метод решения составленной системы уравнений. Провести математическое моделирование протекающих процессов.
• Физический. Устанавливает связь между физическими процессами при деформации с учитыванием физических параметров материала и возникшими напряжениями (механическими качествами).

На математическом и физическом шаге рассмотрения установленной задачи используются следующие главные расчетные выражения и допущения:

• закон Гука для деформации смещения;
• гипотезы прочности (с учитыванием физических и механических параметров материала который для него выбран);
• выбор системы равноценных стрессов;
• упрощения при изображении эпюр, отображающих направления действующих сил и возникших стрессов;
• принятие ключевых положений для случая чистого сдвига.

В первом варианте происходит пластическая дефармация детали, когда интенсивность возникших стрессов превосходит предел текучести материала который для него выбран. Размер подобной деформации зависят от характера и интенсивности действия внешних сил, прочностных показателей материала, изменения режима температур.

При интенсивности влияния, превышающем крепость материала, происходит разрыв. Оба эти процесса приводят к нарушению механических соединений деталей (к примеру, крепежных изделий, заклёпок, втулок).

Разработанные методы расчёта прочности дают возможность проектировать и делать детали с заданием, превышающим этот предел. Это дает возможность значительно повысить прочность и долговечность всей конструкции. Сейчас разработан стройный математический аппарат создания моделей допустимой деформации. Его реализуют с использованием созданных программных средств, которые дают возможность получить числовые характеристики прочности и выстроить графические изображения эпюр в формате 3D графики.

Если вы нашли погрешность, пожалуйста, выдилите фрагмент текста и нажмите Ctrl+Enter.