Модуль зубьев зубчатого колеса

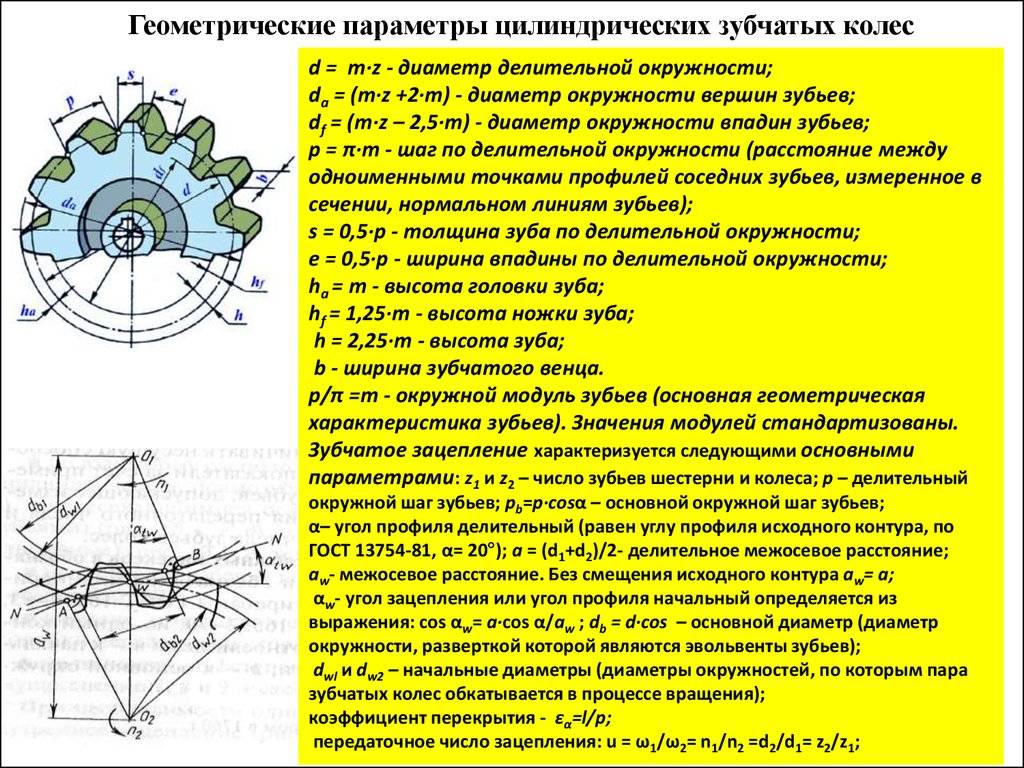
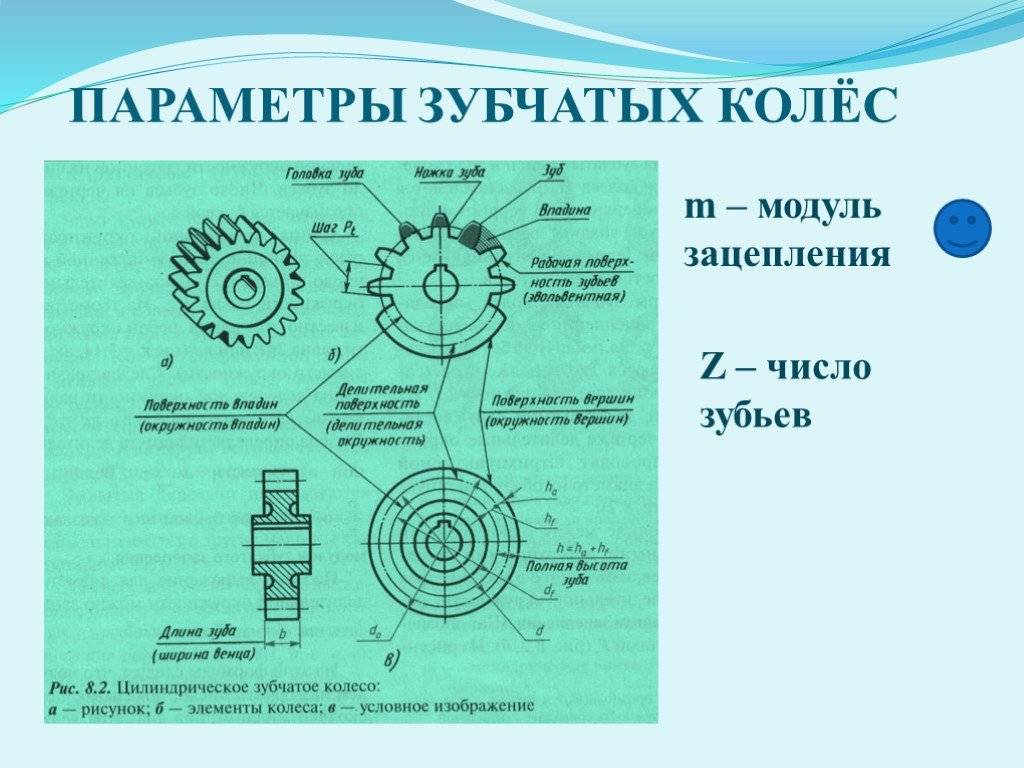
В чем заключаются сходства между шестерней и зубчатым колесом

Между шестерней и зубчатым колесом можно отметить несколько схожих моментов:

• Как и шестерня, зубчатое колесо может быть как ведомым, так и ведущим элементом в общей системе.
• У шестерни и у зубчатого колеса форма может быть как цилиндрической, так и конической, все зависит от той функции, которую конкретная деталь выполняет.
• При помощи шестеренки и зубчатого колеса можно маневрировать на почве скорости вращательного элемента, либо уменьшая ее, либо увеличивая.
• Шестеренки и зубчатые колеса одинаково эффективно можно использовать на электрических и бензоинструментах, однако больше всего используют именно шестеренки, так как они обеспечивают устойчивость механизма.
• Шестеренка и зубчатое колесо могут использоваться для запуска вращательных осей.

Внешние сходства между шестеренкой и зубчатым колесом обоснованы также еще тем, что зачастую эти два элемента могут выполнять схожие функции и быть взаимозаменяемыми в определенных системах и механизмах.

Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

Расчет модуля зубчатого колеса

Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:

проведя преобразование, получим:

Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:

выполнив преобразование, находим:

Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов De получается равным

где h’- высота головки.

Высоту головки приравнивают к m:

Проведя математические преобразования с подстановкой, получим:

Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца:

где h“- высота ножки зубца.

Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

Устройство зубчатого колеса

Выполнив подстановку в правой части равенства, имеем:

что соответствует формуле:

и если выполнить подстановку, то получим:

Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.

Следующий важный размер, толщину зубца s принимают приблизительно равной:

• для отлитых зубцов: 1,53m:
• для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины

• для отлитых зубцов: sв=πm-1,53m=1,61m:
• для выполненных путем фрезерования- sв= πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

• усилия, прикладываемые к детали при эксплуатации;
• конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.

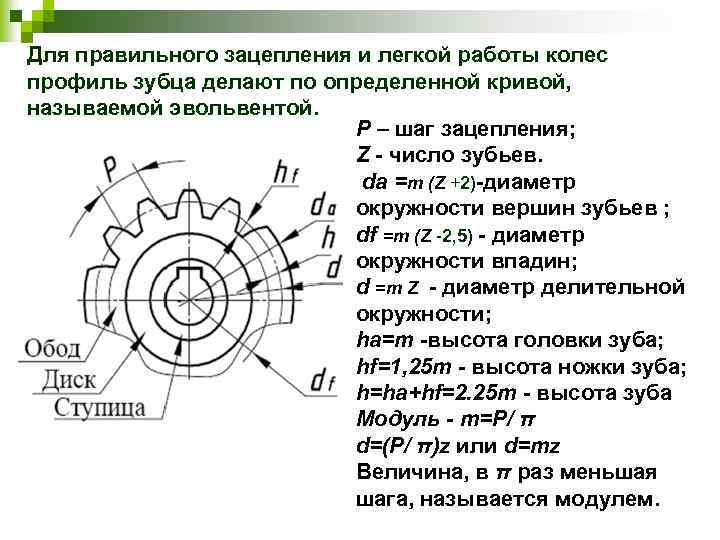
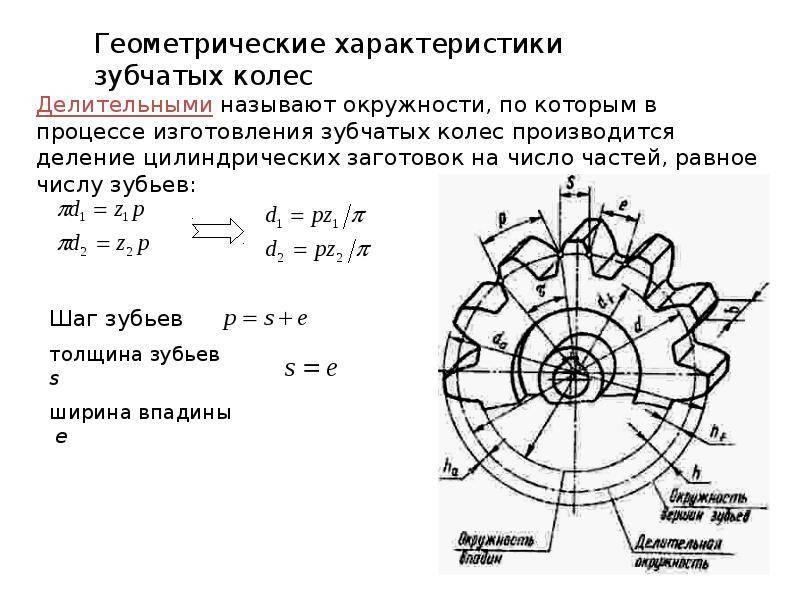
Цилиндрические зубчатые колёса [ править | править код ]

Профиль зубьев колёс как правило имеет эвольвентную боковую форму. Однако существуют передачи с круговой формой профиля зубьев (передача Новикова с одной и двумя линиями зацепления) и с циклоидальной. Кроме того, в храповых механизмах применяются зубчатые колёса с несимметричным профилем зуба.

Параметры эвольвентного зубчатого колеса:

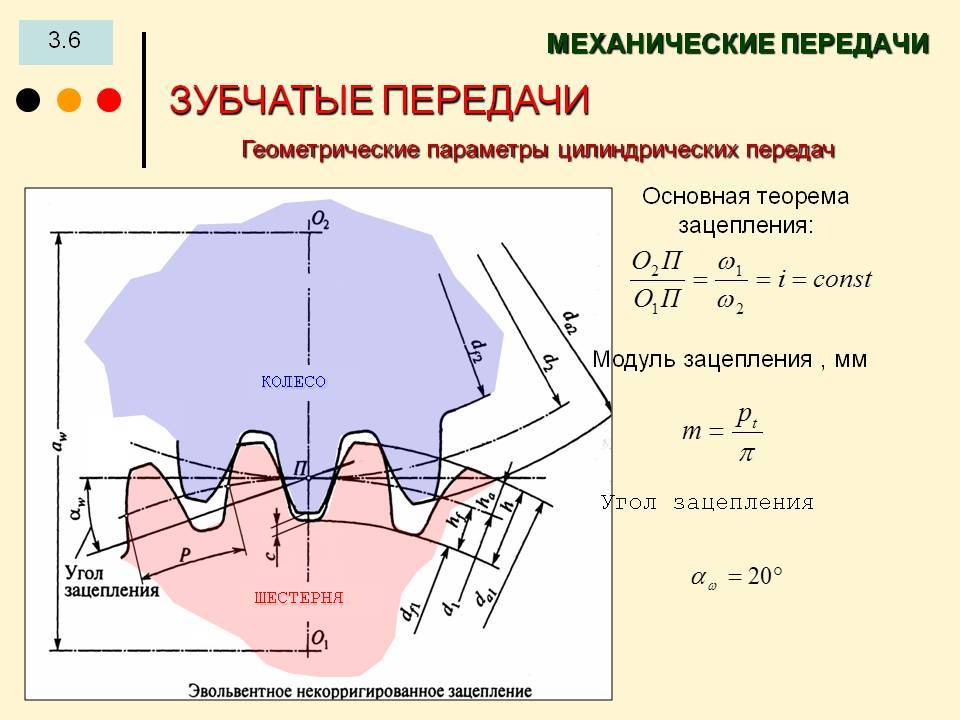
m — модуль колеса. Модулем зацепления называется линейная величина в π раз меньшая окружного шага P или отношение шага по любой концентрической окружности зубчатого колеса к π, то есть модуль — число миллиметров диаметра делительной окружности приходящееся на один зуб. Тёмное и светлое колёсо имеют одинаковый модуль. Самый главный параметр, стандартизирован, определяется из прочностного расчёта зубчатых передач. Чем больше нагружена передача, тем выше значение модуля. Через него выражаются все остальные параметры. Модуль измеряется в миллиметрах, вычисляется по формуле:

>> >

• z — число зубьев колеса
• p — шаг зубьев (отмечен сиреневым цветом)
• d — диаметр делительной окружности (отмечена жёлтым цветом)
• d_a — диаметр окружности вершин тёмного колеса (отмечена красным цветом)
• d_b — диаметр основной окружности — эвольвенты (отмечена зелёным цветом)
• d_f — диаметр окружности впадин тёмного колеса (отмечена синим цветом)
• h_aP+h_fP — высота зуба тёмного колеса, x+h_aP+h_fP — высота зуба светлого колеса

В машиностроении приняты определённые значение модуля зубчатого колеса m для удобства изготовления и замены зубчатых колёс, представляющие собой целые числа или числа с десятичной дробью: 0,5; 0,7; 1; 1,25; 1,5; 1,75; 2; 2,5; 3; 3,5; 4; 4,5; 5 и так далее до 50. (подробнее см. ГОСТ 9563-60 Колеса зубчатые. Модули)

Высота головки зуба — h_aP и высота ножки зуба — h_fP — в случае т. н. нулевого зубчатого колеса (изготовленного без смещения, зубчатое колесо с «нулевыми» зубцами) (смещение режущей рейки, нарезающей зубцы, ближе или дальше к заготовке, причем смещение ближе к заготовке наз. отрицательным смещением, а смещение дальше от заготовки наз. положительным) соотносятся с модулем m следующим образом: h_aP = m; h_fP = 1,25 m, то есть:

h f P h a P = 1 , 25 >>>=1,25> >

Отсюда получаем, что высота зуба h (на рисунке не обозначена):

h = h f P + h a P = 2 , 25 m >+>=2,25m> >

Вообще из рисунка ясно, что диаметр окружности вершин d_a больше диаметра окружности впадин d_f на двойную высоту зуба h. Исходя из всего этого, если требуется практически определить модуль m зубчатого колеса, не имея нужных данных для вычислений (кроме числа зубьев z), то необходимо точно измерить его наружный диаметр d_a и результат разделить на число зубьев z плюс 2:

m = d a z + 2 >> >

Продольная линия зуба

Зубчатые колеса классифицируются в зависимости от формы продольной линии зуба на:

17. Длина общей нормали цилиндрических прямозубых колес

Измерение толщины зубьев при длине общей нормали W имеет то преимущество перед измерением по постоянной хорде, что не требуется более точного изготовления зубчатых колес по наружному диаметру.

Для прямозубых колес без смещения

для колес со смешением (при коэффициенте смещения х)

здесь W’ — длина общей нормали цилиндрических прямозубых колес при m_n = 1. Значения W’ в зависимости от числа зубьев колеса и числа зубьев, охватываемых при измерении, указаны в таблице, приведенной ниже.

Дайна общей нормали W’ цилиндрических прямозубых колес при m_n = 1 мм

Зубчатые передачи

Достоинства: практически неограниченная передаваемая мощность малые габариты и вес стабильное передаточное отношение высокий КПД, который составляет в среднем 0,97 — 0,98

Недостатки: шум в работе на высоких скоростях (может быть снижен при применении зубьев соответствующей геометрической формы и улучшении качества обработки профилей зубьев)

Преимущественное распространение получили передачи с зубьями эвольвентного профиля, которые изготавливаются массовым методом обкатки на зубофрезерных или зубодолбежных станках. Достоинство эвольвентного зацепления состоит в том, что оно мало чувствительно к колебанию межцентрового расстояния

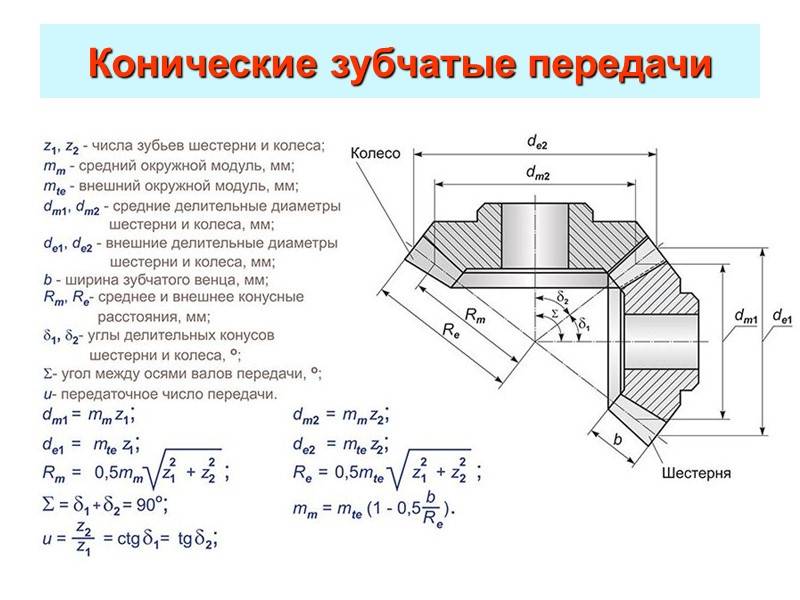
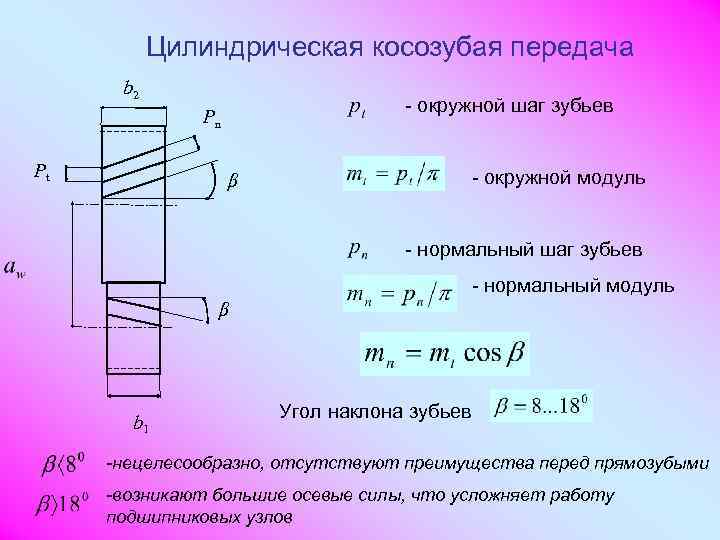
При высоких угловых скоростях вращения рекомендуется применять косозубые шестерни, в которых зубья входят о зацепление плавно, что и обеспечивает относительно бесшумную работу. Недостатком косозубых шестерен является наличие осевых усилий, которые дополнительно нагружают подшипники. Этот недостаток можно устранить, применив сдвоенные шестерни с равнонаправленными спиралями зубьев или шевронные шестерни. Шевронные шестерни, ввиду высокой стоимости и трудности изготовления применяются сравнительно редко — лишь для уникальных передач большой мощности. При малых угловых скоростях вращения применяются конические прямозубые шестерни, при больших — шестерни с круговым зубом, которые в настоящее время заменили конические косозубые шестерни, применяемые ранее. Конические гипоидные шестерни тоже имеют круговой зуб, однако оси колес в них смещены, что создает особенно плавную и бесшумную работу. Передаточное отнесение в зубчатых парах колеблется в широких пределах, однако обычно оно равно 3 — 5

Геометрический расчёт зубчатых колёс

В результате геометрического расчета прямозубых цилиндрических колес (без смещения) определим следующие их параметры (рисунок 2): межосевое расстояние , модуль зубьев m, числа зубьев шестерни z₁ и колеса z₂, делительные диаметры шестерни и колеса , диаметры окружности вершин и , диаметры окружности впадин и , ширина венцов колеса и шестерни .

Рисунок 2 — Параметры цилиндрических колес

1) Рассчитаем предварительно межосевое расстояние, выбрав коэффициент ширины колеса =0,4; полагая, что пара расположена симметрично опорам:

,

где К_а – коэффициент, для прямозубой передачи К_а = 495 МПа 1/3 ;

u – передаточное число редуктора, u = ……;

T₂ – вращающий момент на валу колеса, T₂ = …. Н·м;

[σ_H] — допускаемое контактное напряжение, [σ_H] = 491 МПа;

– коэффициент ширины венца зубчатого колеса, рекомендуемые значения = 0,4;

– коэффициент неравномерности распределения нагрузки по ширине венца зубчатого колеса, определяемый в зависимости от расположения колеса по отношению к опорам и коэффициента ширины колеса =1,3

.

2) Найдем предварительно делительный диаметр шестерни

.

3) Зададим число зубьев шестерни, учитывая, что z_min =17:

4) Подберем из стандарта величину модуля зубьев, для этого предварительно рассчитаем

Из ГОСТ 9563-60 (стандартный ряд m: 1; 1,25; 1,5; 1,75; 2; 2,25; 2,5; 2,75; 3; 3,5; 4; 4,5; 5; 5,5; 6; 7)

мм.

5) Найдем число зубьев сопряженного колеса

,

6) Рассчитаем геометрические параметры проектируемой передачи при

модуле зубьев m=2,25 мм,

числах зубьев шестерни z₁=17 и колеса z₂=71:

Фактическое передаточное число

Отклонение от заданного передаточного числа

Диаметры делительных окружностей

,

,

(если надо задать в п.3) большее число z₁ (18, 19, 20 – 30))

Диаметры окружностей вершин

,

,

Диаметры окружностей впадин

,

,

Ширину венца шестерни назначаем больше ширины венца колеса с целью облегчения сборки механизма.

мм,

мм,

В таблице 2 приведены основные параметры передачи.

Окружная скорость вращения колёс в полюсе зацепления (на делительном диаметре)

.

По рекомендациям (табл. 2.5 в ) принимаем степень точности изготовления зубчатых колес 9-В (ГОСТ 1643-81), что означает 9-ю степень кинематической точности, плавности и контакта зубьев; вид сопряжения В (нормальный боковой зазор).

Таблица 2 — Основные параметры передачи

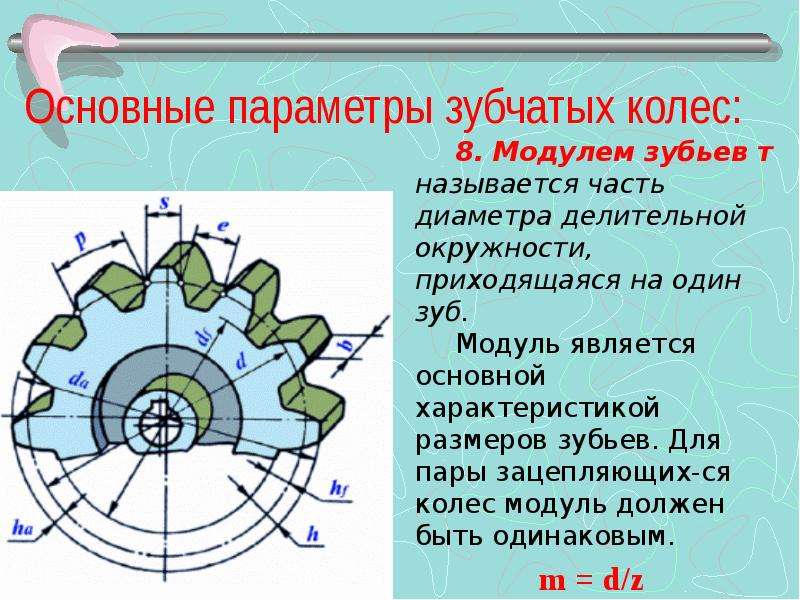
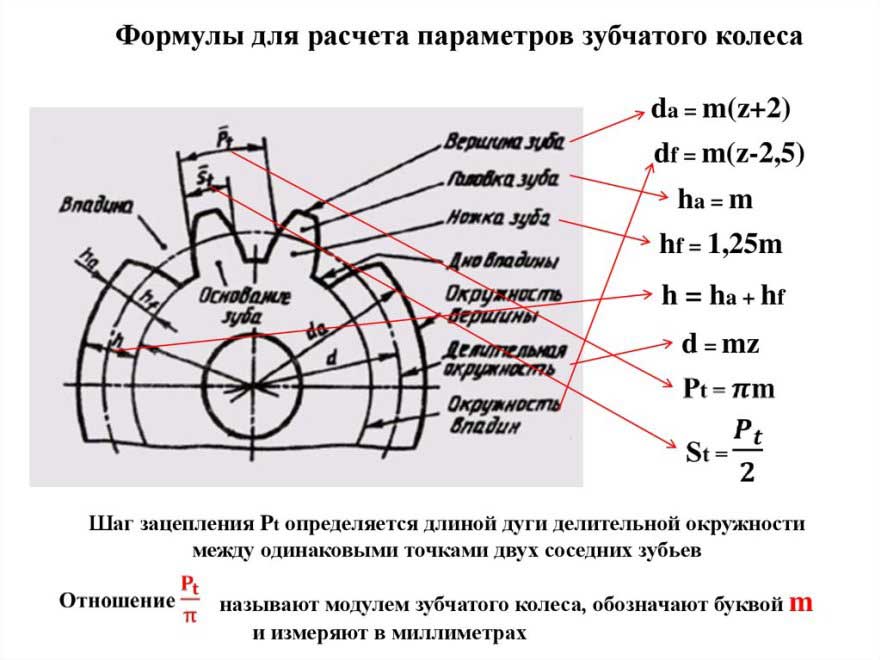
Что такое модуль зубчатого колеса

Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров

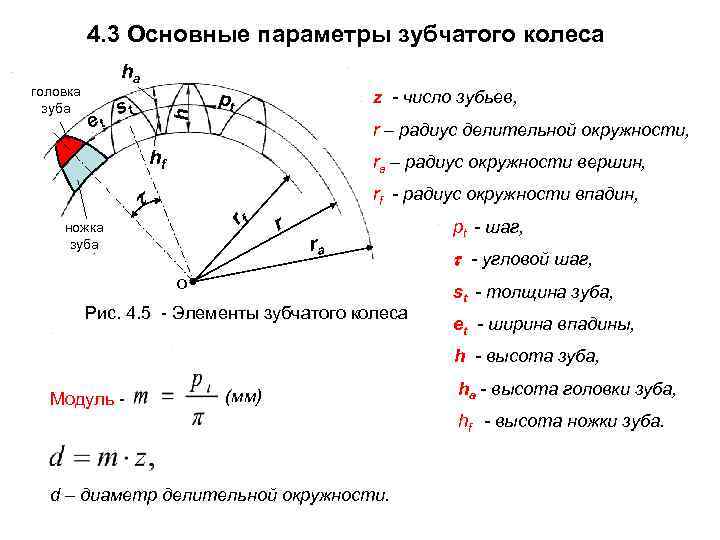
• диаметр;
• число зубьев;
• шаг;
• высота зубца;
• и некоторые другие.

Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида – основной и торцевой.

В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров. Для расчета этого параметра применяют следующие формулы:

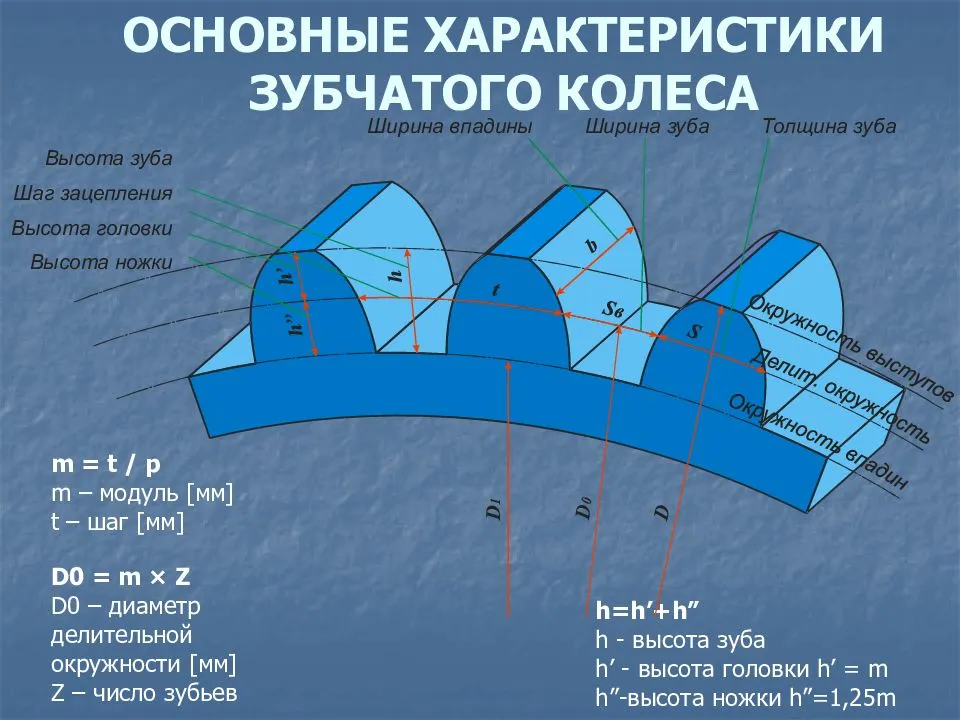
m=t/π,

где t – шаг. Модуль зубчатого колеса можно рассчитать и следующим образом:

m=h/2,25,

где h – высота зубца. И, наконец,

m=De/(z+2),

где De – диаметр окружности выступов,а z – число зубьев.

Что же такое модуль шестерни?

это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.

Цилиндрические зубчатые колёса [ править | править код ]

Профиль зубьев колёс как правило имеет эвольвентную боковую форму. Однако существуют передачи с круговой формой профиля зубьев (передача Новикова с одной и двумя линиями зацепления) и с циклоидальной. Кроме того, в храповых механизмах применяются зубчатые колёса с несимметричным профилем зуба.

Параметры эвольвентного зубчатого колеса:

m — модуль колеса. Модулем зацепления называется линейная величина в π раз меньшая окружного шага P или отношение шага по любой концентрической окружности зубчатого колеса к π, то есть модуль — число миллиметров диаметра делительной окружности приходящееся на один зуб. Тёмное и светлое колёсо имеют одинаковый модуль. Самый главный параметр, стандартизирован, определяется из прочностного расчёта зубчатых передач. Чем больше нагружена передача, тем выше значение модуля. Через него выражаются все остальные параметры. Модуль измеряется в миллиметрах, вычисляется по формуле:

m = d z = p π <displaystyle mathbf >=<frac

<pi >>> >

• z — число зубьев колеса
• p — шаг зубьев (отмечен сиреневым цветом)
• d — диаметр делительной окружности (отмечена жёлтым цветом)
• d_a — диаметр окружности вершин тёмного колеса (отмечена красным цветом)
• d_b — диаметр основной окружности — эвольвенты (отмечена зелёным цветом)
• d_f — диаметр окружности впадин тёмного колеса (отмечена синим цветом)
• h_aP+h_fP — высота зуба тёмного колеса, x+h_aP+h_fP — высота зуба светлого колеса

В машиностроении приняты определённые значение модуля зубчатого колеса m для удобства изготовления и замены зубчатых колёс, представляющие собой целые числа или числа с десятичной дробью: 0,5; 0,7; 1; 1,25; 1,5; 1,75; 2; 2,5; 3; 3,5; 4; 4,5; 5 и так далее до 50. (подробнее см. ГОСТ 9563-60 Колеса зубчатые. Модули)

Высота головки зуба — h_aP и высота ножки зуба — h_fP — в случае т. н. нулевого зубчатого колеса (изготовленного без смещения, зубчатое колесо с «нулевыми» зубцами) (смещение режущей рейки, нарезающей зубцы, ближе или дальше к заготовке, причем смещение ближе к заготовке наз. отрицательным смещением, а смещение дальше от заготовки наз. положительным) соотносятся с модулем m следующим образом: h_aP = m; h_fP = 1,25 m, то есть:

h f P h a P = 1 , 25 <displaystyle mathbf <<frac >>>=1,25> >

Отсюда получаем, что высота зуба h (на рисунке не обозначена):

h = h f P + h a P = 2 , 25 m <displaystyle mathbf >+>=2,25m> >

Вообще из рисунка ясно, что диаметр окружности вершин d_a больше диаметра окружности впадин d_f на двойную высоту зуба h. Исходя из всего этого, если требуется практически определить модуль m зубчатого колеса, не имея нужных данных для вычислений (кроме числа зубьев z), то необходимо точно измерить его наружный диаметр d_a и результат разделить на число зубьев z плюс 2:

m = d a z + 2 <displaystyle mathbf >> >

Общее определение

Наглядный пример изменения числа оборотов проще всего наблюдать на простом велосипеде. Человек медленно крутит педали. Колесо вращается значительно быстрее. Изменение количества оборотов происходит за счет 2 звездочек, соединенных в цепь. Когда большая, вращающаяся вместе с педалями, делает один оборот, маленькая, стоящая на задней ступице, прокручивается несколько раз.

Передачи с крутящим моментом

В механизмах используют несколько видов передач, изменяющих крутящий момент. Они имеют свои особенности, положительные качества и недостатки. Наиболее распространенные передачи:

Ременная передача самая простая в исполнении. Используется при создании самодельных станков, в станочном оборудование для изменения скорости вращения рабочего узла, в автомобилях.

Ремень натягивается между 2 шкивами и передает вращение от ведущего в ведомому. Производительность низкая, поскольку ремень скользит по гладкой поверхности. Благодаря этому, ременной узел является самым безопасным способом передавать вращение. При перегрузке происходит проскальзывание ремня, и остановка ведомого вала.

Передаваемое количество оборотов зависит от диаметра шкивов и коэффициента сцепления. Направление вращения не меняется.

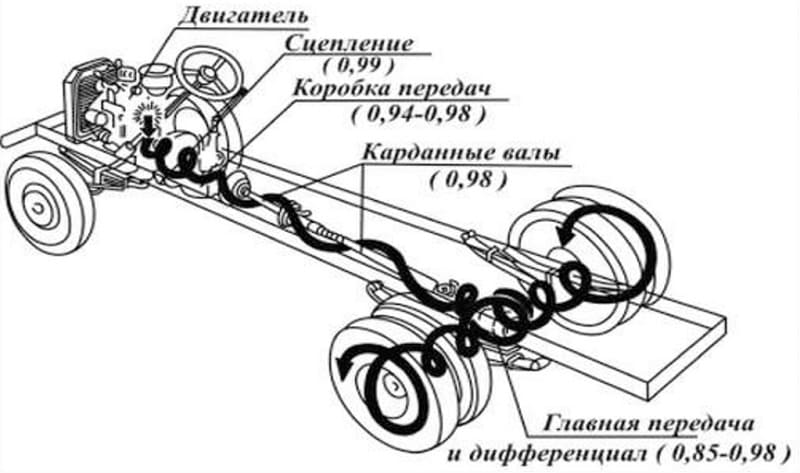
На ремне имеются выступы, на шестерне зубчики. Такой тип ремня расположен под капотом автомобиля и связывает звездочки на осях коленвала и карбюратора. При перегрузе ремень рвется, так как это самая дешевая деталь узла.

Цепная состоит из звездочек и цепи с роликами. Передающееся число оборотов, усилие и направление вращения не меняются. Цепные передачи широко применяются в транспортных механизмах, на конвейерах.

Характеристика зубчатой передачи

В зубчатой передаче ведущая и ведомая детали взаимодействуют непосредственно, за счет зацепления зубьев. Основное правило работы такого узла – модули должны быть одинаковыми. В противном случае механизм заклинит. Отсюда следует, что диаметры увеличиваются в прямой зависимости от количества зубьев. Одни значения можно в расчетах заменить другими.

Например, между осями или точками на эвольвенте по средней линии Размер модуля состоит из ширины зуба и промежутка между ними. Измерять модуль лучше в точке пересечения линии основания и оси зубца. Чем меньше радиус, тем сильнее искажается промежуток между зубьями по наружному диаметру, он увеличивается к вершине от номинального размера. Идеальные формы эвольвенты практически могут быть только на рейке. Теоретически на колесе с максимально бесконечным радиусом.

Деталь с меньшим количеством зубьев называют шестерней. Обычно она ведущая, передает крутящий момент от двигателя.

Зубчатое колесо имеет больший диаметр и в паре ведомое. Оно соединено с рабочим узлом. Например, передает вращение с необходимой скоростью на колеса автомобиля, шпиндель станка.

Обычно посредством зубчатой передачи уменьшается количество оборотов и увеличивается мощность. Если в паре деталь, имеющая больший диаметр, ведущая, на выходе шестерня имеет большее количество оборотов, вращается быстрее, но мощность механизма падает. Такие передачи называют понижающими.

Зачем нужна паразитка

При взаимодействии шестерни и колеса происходит изменение сразу нескольких величин:

• количества оборотов;
• мощности;
• направление вращения.

Только в планетарных узлах с нарезкой зубьев по внутреннему диаметру венца сохраняется направление вращения. При наружном зацеплении ставится две одинаковые шестерни подряд. Их взаимодействие не меняет ничего, кроме направления движения. В этом случае обе зубчатые детали называются шестернями, колеса нет. Вторая, промежуточная, получила название «паразитка», поскольку в вычислениях не участвует, меняет только знак.

Виды зубчатых соединений

Зубчатое зацепление может иметь различную форму зуба на деталях. Это зависит от исходной нагрузки и расположения осей сопрягаемых деталей. Различают виды зубчатых подвижных соединений:

Самое распространенное и простое в исполнении прямозубое зацепление. Наружная поверхность зуба цилиндрическая. Расположение осей шестерни и колеса параллельное. Зуб расположен под прямым углом к торцу детали.

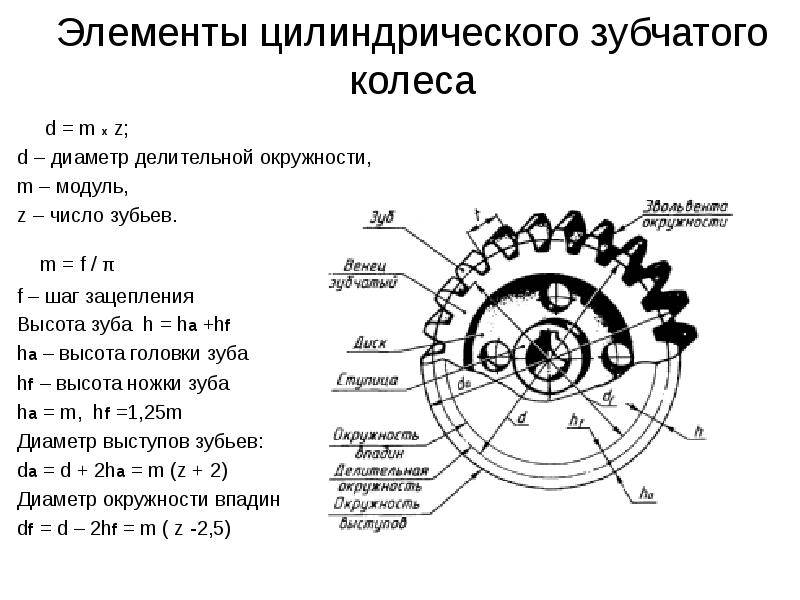
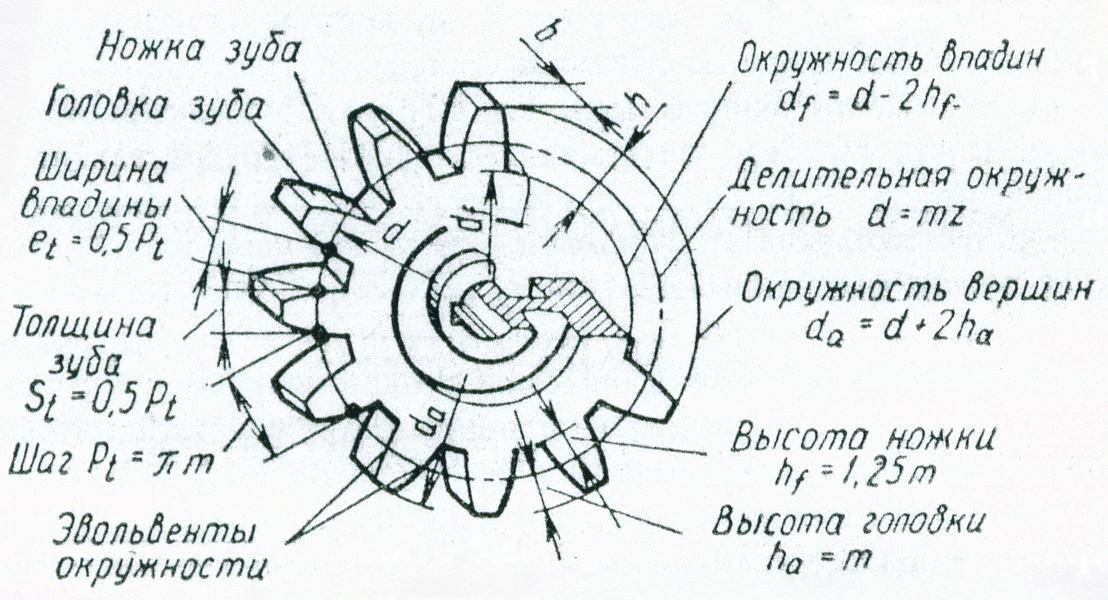
Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D – ее диаметр.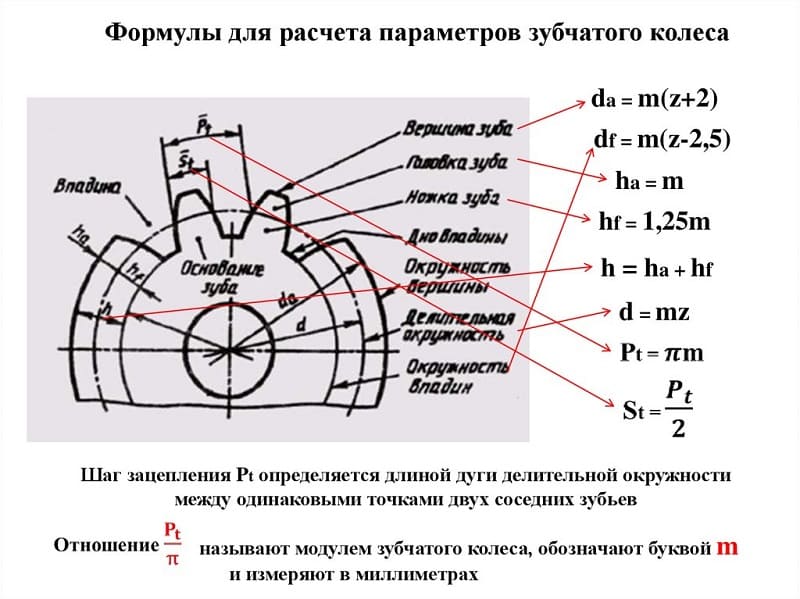Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:

π×D=t×z,

проведя преобразование, получим:

D=(t /π)×z

Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

t/π=m,

размерность модуля шестерни – миллиметры. Если подставить его в предыдущее выражение, то получится:

В=m×z;

выполнив преобразование, находим:

m=D / z.

Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов D_e получается равным

De=d+2× h’,

где h’- высота головки. Высоту головки приравнивают к m:

 h’=m.

Проведя математические преобразования с подстановкой, получим:

De=m×z+2m = m(z+2),

откуда вытекает:

m=De/(z+2).

Диаметр окружности впадин D_i соответствует D_e за вычетом двух высот основания зубца:

D_i=D-2h“,

где h“- высота ножки зубца. Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

h’ = 1,25m.Выполнив подстановку в правой части равенства, имеем:

D_i = m×z-2×1,25m = m×z-2,5m;

что соответствует формуле:

D_i = m(z-2,5m).

Полная высота:

h = h’+h“,

и если выполнить подстановку, то получим:

h = 1m+1,25m=2,25m.

Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25. Следующий важный размер, толщину зубца s принимают приблизительно равной:

• для отлитых зубцов: 1,53m:
• для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины s_в, получаем формулы для ширины впадины

• для отлитых зубцов: s_в=πm-1,53m=1,61m:
• для выполненных путем фрезерования- s_в= πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

• усилия, прикладываемые к детали при эксплуатации;
• конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.

Зубчатая рейка

Зубчатая рейка является частью зубчатого колеса с бесконечным радиусом делительной окружности. Вследствие этого ее окружности представляют собой прямые параллельные линии. Эвольвентный профиль зубчатой рейки тоже имеет прямолинейное очертание. Это свойство эвольвенты является наиболее важным при изготовлении зубчатых колёс. Передачу с применением зубчатой планки (рейки) называют – реечная передача (кремальера), она используется для преобразования вращательного движения в поступательное и наоборот. Состоит передача из зубчатой рейки и прямозубого зубчатого колеса (шестеренки). Применяется такая передача в зубчатой железной дороге.

Основные параметры зубчатых цилиндрических передач

Стандарт распространяется на цилиндрические передачи внешнего зацепления для редукторов и ускорителей, в том числе и комбинированных (коническо-цилиндрических, цилиндро-червячных и др.), выполняемых в виде самостоятельных агрегатов. Стандарт не распространяется на передачи редукторов специального назначения и специальной конструкции Для встроенных передач стандарт является рекомендуемым

Межосевые расстояния

1 ряд	40	50	63	80	100	125	—	160	—	200	—	250	—	315	—	400
2 ряд	—	—	—	—	—	—	140	—	180	—	225	—	280	—	355	—
1 ряд	—	500	—	630	—	800	—	1000	—	1250	—	1600	—	2000	—	2500
2 ряд	450	—	560	—	710	—	900	—	1120	—	1400	—	1800	—	2240	—

1-й ряд следует предпочитать 2-му

Межосевые расстояния для двухступенчатых несоосных редукторов общего назначения

Быстроходная ступень	40	50	63	80	100	125	140	160	180	200	225	250	280	315
Тихоходная ступень	63	80	100	125	160	200	225	250	280	315	355	400	450	500
Быстроходная ступень	355	400	450	500	560	630	710	800	900	1000	1120	1250	1400	1600
Тихоходная ступень	560	630	710	800	900	1000	1120	1250	1400	1600	1800	2000	2240	2500

Коэффициент запаса прочности при работе зуба двумя сторонами

Например: зубья реверсивных передач или зубья сателлитов в планетарных передачах

Материал колес и термо- обработка	Отливки стальные и чугунные без термо- обработки	Отливки стальные и чугунные с термо- обработкой	Поковки стальные нормали- зованные или улучшенные	Поковки и отливки стальные с поверх- ностной закалкой (сердцевина вязкая)	Стальные, нормали- зованные или улучшенные, а также с поверх- ностной закалкой	Стальные с объемной закалкой	Стальные, подверг- нутые цементации, азоти- рованию, циани- рованию и др.	Чугунные и пласт- массовые колеса
Коэфф.	1,9	1,7	1,5	2,2	1,4 — 1,6	1,8	1,2	1 — 1,2

Межосевые расстояния для трехступенчатых несоосных редукторов общего назначения

Быстроходная ступень	40	50	63	80	100	125	140	160	180	200
Промежуточная ступень	63	80	100	125	160	200	225	250	280	315
Тихоходная ступень	100	125	160	200	250	315	355	400	450	500
Быстроходная ступень	225	250	280	315	355	400	450	500	560	630
Промежуточная ступень	355	400	450	500	560	630	710	800	900	1000
Тихоходная ступень	560	630	710	800	900	1000	1120	1250	1400	1600

Номинальные передаточные числа

1 ряд	1,0	—	1,25	—	1,6	—	2,0	—	2,5	—	3,15
2 ряд	—	1,12	—	1,4	—	1,8	—	2,24	—	2,8	—
1 ряд	—	4,0	—	5,0	—	6,3	—	8,0	—	10	—	12,5
2 ряд	3,55	—	4,5	—	5,6	—	7,1	—	9,0	—	11,2	—

1-й ряд следует предпочитать 2-му Фактические значения передаточных чисел не должны отличаться от номинальных более чем на 2,5% при номинальном меньше 4,5 и на 4% при номинальном больше 4,5

Коэффициент ширины зубчатых колес (отношение ширины зубчатого колеса к межосевому расстоянию) должен соответствовать: 0,100; 0,125; 0,160; 0,200; 0,315; 0,400; 0,500; 0,630; 0,800; 1,0; 1,25

Численные значения ширины зубчатых колес округляются до ближайшего числа из ряда Ra20 по ГОСТу 6636.

При различной ширине сопряженных зубчатых колес значение коэффициента ширины зубчатых колес относится к более узкому из них.

Что представляет собой шестерня

Шестерня – это небольшое колесико с зубьями, которое крепится к специальной вращающейся оси. Поверхность у шестеренки в данном случае может быть как конической, так и цилиндрической.

Шестеренчатые передачи также имеют свою классификацию:

1. Прямозубые. Наиболее распространенный вид шестеренок, у которых зубья зачастую располагаются в радиальных плоскостях.
2. Скошенные. По-другому этот тип называется еще косозубым, а его использование в ходу у бензо- и электрических инструментов. По отношению к вращающейся оси они находятся под определенным углом.
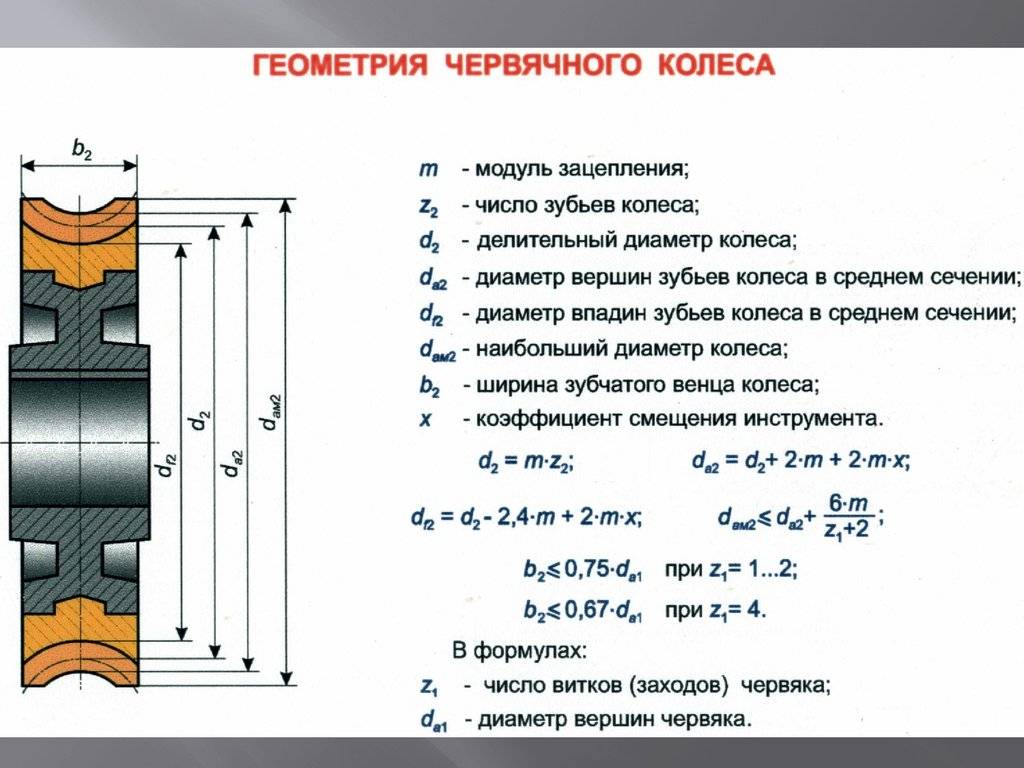
3. Червячные. Их еще называют спиральными шестернями, которые используются преимущественно для рулевого управления автомобилем.
4. Винтовые. Они имеют зачастую форму цилиндра, а также расположены по всей линии винта. Располагаются такие шестеренки на валах, которые расположены перпендикулярно к вращающейся оси.

Данные разновидности являются наиболее распространенными, однако далеко не единственными, поэтому используемый вид напрямую соотносится с тем, какую функцию он должен будет выполнять.

При этом каждая шестеренка имеет определенное количество зубьев, что определяется ее назначением. Разница между количеством используемых зубьев необходима, поскольку благодаря этому фактору появляется возможность регулировать обороты вала и крутящийся момент. Шестеренки также разделяются на ведущие и ведомые. Ведущей называется та шестерня, к которой вращательный момент подводится снаружи, а ведомой – та, с которой она снимается.

Почему шестеренку называют так?

Технически это понятно. Изначально «шестерёнка» — самое маленькое колесо в зубчатой передаче. Меньше шести зубьев там не бывает даже в теории, захват не обепечивается. … В машиностроении ведомое колесо зубчатой передачи редуктора называется колесом».

Характеристики и применение

Зубья шестеренки находятся в радиальных плоскостях. Линия контакта прямозубых цилиндрических шестерней параллельна оси вращения.

В зависимости от необходимых нагрузочных характеристик и точности передаваемого вращения, подбирается модуль (расстояние между центрами зубов) от 1 до 6.

Используется в подвижных частях механизмов соместно с зубчатой рейкой.

Цилиндрическая зубчатая передача применяется во всех типах автоматических ворот, конвейерных линиях с повышенной нагрузкой, 3D принтерах, станках ЧПУ и многом другом.

Параметры модуля шестерни

Рассматриваемая характеристика обозначается литерой m, указывает на прочность зубчатых передач. Единица измеряется в миллиметрах (чем выше нагрузка на передачу, тем больше модульное значение). В расчете параметра используются следующие показатели:

• диаметр делительной окружности;
• шаг и число зубьев;
• эвольвент (диаметр основной окружности);
• аналогичная характеристика впадин темной шестеренки;
• высота зуба темного и светлого колеса.

В машиностроительной отрасли расчеты ведутся по стандартным значениям для удобства изготовления и замены шестерен с числами от 1-го до 50-ти.

Что такое модуль на чертеже?

Модуль — это унифицированный элемент любых систем, состоящий из взаимозаменяемого комплекса деталей массового производства. Чертеж модуля выполняется на основании ГОСТ 2.109-73 — единая система конструкторской документации (ЕСКД).

Коронная шестерня

Коронная шестерня – это особый тип шестерен, их зубья находятся на боковой поверхности. Такая шестерня работает, как правило, в паре с прямозубой или с барабаном (цевочное колесо), состоящим из стержней. Такая передача используется в башенных часах.

Зубча́тое колесо́ или шестерня́ , зубчатка — основная деталь зубчатой передачи в виде диска с зубьями на цилиндрической или конической поверхности, входящими в зацепление с зубьями другого зубчатого колеса.

Обычно термины зубчатое колесо, шестерня, зубчатка являются синонимами, но некоторые авторы называют ведущее зубчатое колесо шестернёй, а ведомое — колесом . Происхождение слова «шестерня́» доподлинно неизвестно, хотя встречаются предположения о связи с числом «шесть». Л. В. Куркина, однако, выводит термин из слова «шест» (в смысле «ось») .

Зубчатые колёса обычно используются па́рами с разным числом зубьев с целью преобразования крутящего момента и числа оборотов валов на входе и выходе. Колесо, к которому крутящий момент подводится извне, называется ведущим, а колесо, с которого момент снимается — ведомым. Если диаметр ведущего колеса меньше, то крутящий момент ведомого колеса увеличивается за счёт пропорционального уменьшения скорости вращения, и наоборот. В соответствии с передаточным отношением, увеличение крутящего момента будет вызывать пропорциональное уменьшение угловой скорости вращения ведомой шестерни, а их произведение — механическая мощность — останется неизменным. Данное соотношение справедливо лишь для идеального случая, не учитывающего потери на трение и другие эффекты, характерные для реальных устройств.

Настройка цепи дифференциала при обработке винтовых изделий.

Типичной является следующая формула:

где с — постоянная цепи;

β — угол наклона винтовой линии;

n — число заходов фрезы.

Продифференцировав обе части равенства, получим абсолютную погрешность di передаточного отношения

тогда допустимая относительная погрешность настройки

Если допустимое отклонение угла винтовой линии dβ выразить не в радианах, а в минутах, то получим

Например, если угол наклона винтовой линии изделия β = 18°, а допустимое отклонение в направлении зуба dβ = 4″ = 0′,067, то допустимая относительная погрешность настройки

δ = 0,067/3440*tg18 = 0,00006

Наоборот, зная относительную погрешность взятого передаточного отношения, можно по формуле (3) определить допущенную погрешность в угле винтовой линии в минутах. При установлении допустимой относительной погрешности можно в подобных случаях пользоваться тригонометрическими таблицами. Так, в формуле (2) передаточное отношение пропорционально sin β. По тригонометрическим таблицам для взятого числового примера видно, что sin 18° = 0,30902, а разность синусов на 1′ составляет 0,00028. Следовательно, относительная погрешность на 1′ составляет 0,00028 : 0,30902 = 0,0009. Допустимое отклонение винтовой линии — 0,067, поэтому допустимая погрешность передаточного отношения 0,0009*0,067 = 0,00006, такая же, как и при расчете по формуле (3). Когда оба сопряженных колеса нарезаются на одном станке и по одной настройке цепи дифференциала, то погрешности в направлении линий зубьев допускаются значительно большие, так как у обоих колес отклонения одинаковы и незначительно влияют только на боковой зазор при зацеплении сопряженных колес.