Линейчатые поверхности

7.6. Сферическая поверхность

Сферическая поверхность – поверхность, образованная вращением окружности вокруг отрезка, являющегося её диаметром.

Шаром называется тело, ограниченное сферической поверхностью.

Экватор – это окружность, которая получается пересечением сферы горизонтальной плоскостью, проходящей через ее центр (Рисунок 7.10).

Меридиан – это окружность, которая получается пересечением сферы плоскостью, перпендикулярной плоскости экватора и проходящей через центр сферы.

Параллелями называются окружности, которые получаются пересечением сферы плоскостями, параллельными плоскости экватора.

Рисунок 7.10 – Проецирование сферической поверхности

Прямоугольная проекция шара (сферы) на любую плоскость – есть окружность, которую часто называют очерковой.

Рисунок 7.11 – Эпюр сферы и принадлежащих ей точек

Линейчатые поверхности. Принадлежность линии и точки к поверхности

Линейчатой называется поверхность, образующей которой является прямая линия.

В общем случае линейчатая поверхность однозначно определяется тремя направляющими линиями .

Задать поверхность на чертеже – значит указать условия, позволяющие построить каждую точку этойповерхности. Для задания поверхности достаточно иметь проекции направляющей линии и указать, как строится образующая прямая, проходящая через любую точку направляющей. Однако, для придания наглядности изображения, вычерчивают очерк, линии видимости и строят точки на поверхности.

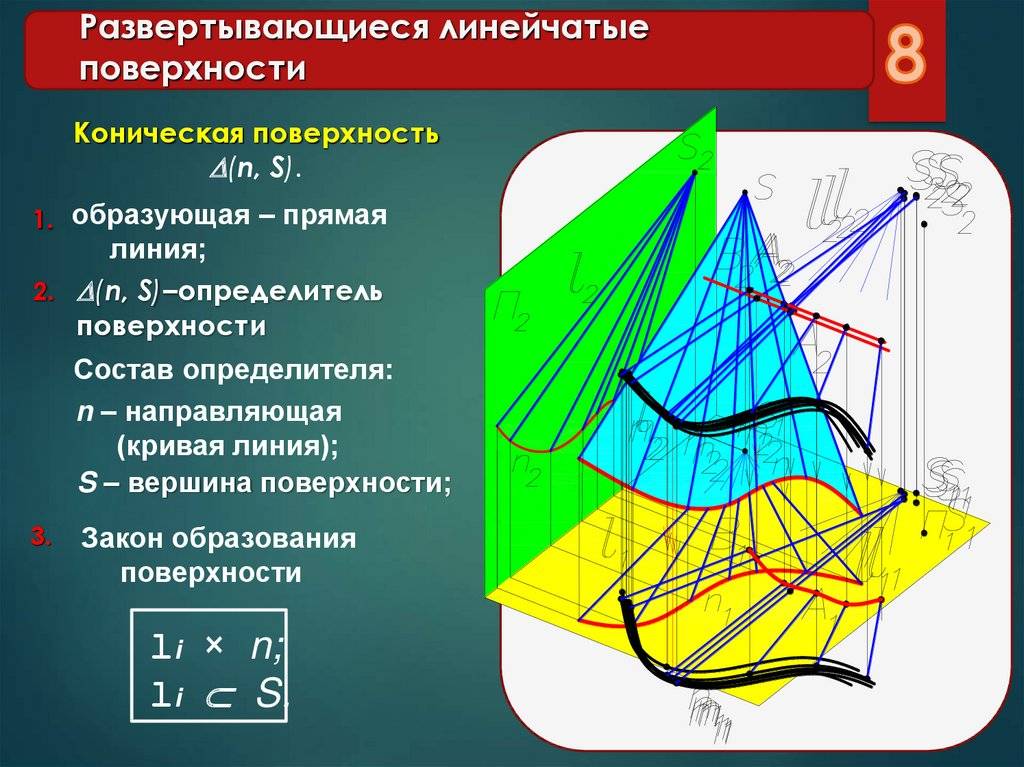
Коническая поверхность образуется прямой линией, проходящей через некоторую неподвижную точку и последовательно через все точки некоторой кривой направляющей линии. Если направляющей линией является окружность, то поверхность называется наклонным или эллиптическим конусом.

На рис. 3.10 представлены: направляющая окружность – m; неподвижная точка – S; прямолинейная образующая — l . Это первая часть определителя – геометрическая. Образующая движется по направляющей, оставаясь неподвижной в точке S. Описание закона движения является алгоритмической частью определителя. При этих условиях поверхность на чертеже считается заданной. Для придания наглядности, на рис. 3.11 построены очертания поверхности, линии видимости и промежуточная точка, принадлежащая поверхности.

Построение точек, принадлежащих поверхности, осуществляется следующим образом. Пусть задана фронтальная проекция точки А (А»). На фронтальной плоскости она изображена как невидимая. Для построения ее горизонтальной проекции через точку задаем линию, принадлежащую поверхности. Этой линией будет окружность, так как линия задана параллельно основанию, а основанием является окружность. Центр окружности лежит на осевой линии поверхности. Проводим линию связи из центра окружности на горизонтальную плоскость до пересечения с горизонтальной осевой поверхности. Строим окружность, которой принадлежит точка А.. По линии связи отмечаем ее местоположение с учетом видимости для горизонтальной плоскости, где точка является видимой. Аналогичные построения выполняются для наклонного (эллиптического) цилиндра.

Тема 4

Позиционные задачи

Все задачи начертательной геометрии условно могут быть разделены на метрические и позиционные. К метрическим задачам относятся задачи на измерение линейных и угловых величин. Решение этих задач будет рассмотрено ниже.

К позиционным задачам относятся задачи на принадлежность и взаимное пересечение геометрических фигур. По существу решение позиционных задач сводится к нахождению точек одновременно принадлежащих двум или более фигурам. Задачи на определение принадлежности одной геометрической фигуры к другой частично уже рассмотрены:

o принадлежность точки к прямой (рис. 1.23) .

o принадлежность линии к поверхности. Рис. 3.9 ;

o принадлежность точки к поверхности. Рис. 3.11

Задачи на построение линий пересечения геометрических фигур условно можно разделить на три группы:

o пересечение плоскости с поверхностью;

o пересечение прямой линии с плоскостью и с поверхностью.

o взаимное пересечение поверхностей.

Решение всех типов позиционных задач на пересечение подчиняются общему алгоритму. На рис. 4.1 представлена поверхность полусферы и усеченного конуса. Для построения точек, одновременно принадлежащих этим поверхностям, воспользуемся общим алгоритмом.

1. Вводится вспомогательная поверхность, в частном случае — плоскость. Эта вспомогательная поверхность назначается таким образом, чтобы она пересекла обе фигуры по простым для построения линиям — по прямым или по окружностям.

2. Строятся линии пересечения вспомогательной поверхности с каждой из заданных фигур.

3. Отмечаются точки взаимного пересечения построенных линий. Эти точки принадлежат обеим фигурам, следовательно, являются элементом пересечения фигур.

4. Соединяют точки в определенной последовательности и определяют видимость линии пересечения и фигур друг относительно друга.

Находить точки для построения линии взаимного пересечения фигур надо в определенной последовательности.

1. В первую очередь отмечают точки на контурных образующих или на ребрах, если поверхностигранные.

2. Находят экстремальные точки: наивысшую; наинизшую; самую левую; самую правую; самую ближнюю и самую дальнюю.

3. Отмечают точки на линиях среза (принадлежащие основаниям).

4. Если построенных точек недостаточно для выявления формы линии взаимного пересечения, строят ряд промежуточных (случайных) точек.

голоса

Рейтинг статьи

Касательные плоскости, развертываемые поверхности

Для необходимых здесь выводов всегда предполагается, что они также существуют.

Чтобы вычислить вектор нормали в точке, нужны частные производные представления  : Икс(ты,v)знак равноc(ты)+vр(ты){\ displaystyle \ quad \ mathbf {x} (u, v) = \ mathbf {c} (u) + v \; \ mathbf {r} (u)}

Икстызнак равноc˙(ты)+vр˙(ты) {\ displaystyle \ mathbf {x} _ {u} = \ mathbf {\ dot {c}} (u) + v \; \ mathbf {\ dot {r}} (u) \} ,Иксvзнак равнор(ты){\ displaystyle \ quad \ mathbf {x} _ {v} = \; \ mathbf {r} (u)}

пзнак равноИксты×Икстызнак равноc˙×р+v(р˙×р) .{\ displaystyle \ mathbf {n} = \ mathbf {x} _ {u} \ times \ mathbf {x} _ {u} = \ mathbf {\ dot {c}} \ times \ mathbf {r} + v (\ mathbf {\ dot {r}} \ times \ mathbf {r}) \.}

Поскольку скалярное произведение (позднее произведение с двумя равными векторами всегда равно 0!), В каждой точке есть касательный вектор . Касательные плоскости вдоль этой прямой идентичны, если они кратны . Это возможно только в том случае, если три вектора лежат в одной плоскости, т.е. ЧАС. линейно зависимы. Линейную зависимость трех векторов можно определить с помощью определителя этих векторов: п⋅рзнак равно{\ Displaystyle \ mathbf {п} \ cdot \ mathbf {r} = 0}р(ты){\ Displaystyle \ mathbf {r} (и_ {0})}Икс(ты,v){\ Displaystyle \ mathbf {х} (и_ {0}, v)}р˙×р{\ displaystyle \ mathbf {\ dot {r}} \ times \ mathbf {r}}c˙×р{\ displaystyle \ mathbf {\ dot {c}} \ times \ mathbf {r}}c˙,р˙,р {\ Displaystyle \ mathbf {\ точка {с}} \ ;, \; \ mathbf {\ точка {r}} \ ;, \; \ mathbf {r} \}

Касательные плоскости вдоль прямой совпадают, еслиИкс(ты0,v)знак равноc(ты0)+vр(ты0){\ displaystyle \ mathbf {x} (u_ {0}, v) = \ mathbf {c} (u_ {0}) + v \; \ mathbf {r} (u_ {0})}

Det(c˙(ты),р˙(ты),р(ты))знак равно .{\ displaystyle \ det (\ mathbf {\ dot {c}} (u_ {0}) \ ;, \; \ mathbf {\ dot {r}} (u_ {0}) \ ;, \; \ mathbf {r } (u_ {0})) \; = \; 0 \.}

Генеративная форма, к которой это применимо, называется торсальной .

Линейчатая поверхность точно тогда раскручивается в плоскость, когда для всех точек гауссова кривизна равна нулю. Это так тогда и только тогда, когдаИкс(ты,v)знак равноc(ты)+vр(ты){\ displaystyle \ quad \ mathbf {x} (u, v) = \ mathbf {c} (u) + v \; \ mathbf {r} (u)}

Det(c˙,р˙,р)знак равно{\ displaystyle \ det (\ mathbf {\ dot {c}} \; \; \ mathbf {\ dot {r}} \ ;, \; \ mathbf {r}) \; = \; 0 \ quad}

применяется в каждой точке, d. т. е. если каждый образующий – торсальный. Поэтому развивающуюся область также называют торсом .

Свойства развертывающейся поверхности:

• Генераторы представляют собой семейство асимптотических линий , а также семейство линий кривизны .
• Разворачивающаяся поверхность – это либо (общий) цилиндр, либо (общий) конус, либо касательная поверхность (поверхность, состоящая из касательных пространственной кривой).

Линейчатые поверхности в алгебраической геометрии

В алгебраической геометрии линейчатые поверхности изначально определялись как проективные поверхности в проективном пространстве , содержащие прямую линию, проходящую через любую заданную точку. Отсюда сразу следует, что на поверхности существует проективная прямая, проходящая через любую заданную точку, и это условие теперь часто используется в качестве определения линейчатой ​​поверхности: линейчатые поверхности определяются как абстрактные проективные поверхности, удовлетворяющие этому условию существования проективной прямой. через любую точку. Это эквивалентно утверждению, что они бирациональны произведению кривой и проективной прямой. Иногда линейчатая поверхность определяется как поверхность, удовлетворяющая более сильному условию, состоящему в том, что она имеет расслоение .над кривой со слоями, являющимися проективными прямыми. Это исключает проективную плоскость, которая имеет проективную прямую через каждую точку, но не может быть записана как такое расслоение.

Линейчатые поверхности появляются в классификации проективных комплексных поверхностей Энриквеса, потому что каждая алгебраическая поверхность размерности Кодаиры −∞{\ Displaystyle – \ infty}является линейчатой ​​поверхностью (или проективной плоскостью, если использовать ограничительное определение линейчатой ​​поверхности). Каждая минимальная проективная линейчатая поверхность, отличная от проективной плоскости, является проективным расслоением двумерного векторного расслоения над некоторой кривой. Линейчатые поверхности с базовой кривой рода 0 являются поверхностями Хирцебруха .

Решение задач

Задание 1 (Феденко 535)

Написать уравнение цилиндрической поверхности, для которой линия $\vec{\rho}=\vec{\rho}(u)$ является направляющей, а образующие параллельны вектору $\vec{e}$.
\begin{equation*}
\vec{R}=\vec{\rho}(u)+v\vec{e}.
\end{equation*}

Задание 2 (Феденко 536)

Напишите параметрические уравнения цилиндрической поверхности, образующие которой параллельны вектору $\vec{a}=\{1,2,3\}$, а направляющая задана уравнениями: $x=u$, $y=u^2$, $z=u^3$.

Направляющая: $\vec{\rho}=\{u, u^2, u^3\}$,

Образующая: $\vec{\mu}=\{1,2,3\}$,

Уравнение:
\begin{equation*}
\vec{R}=\vec{\rho}(u)+v\vec{e}.
\end{equation*}
\begin{equation*}
\left\{
\begin{aligned}
&x=u+v, \\
&y=u^2+2v,\\
&z=u^3+3v.
\end{aligned}
\right.
\end{equation*}

Задание 3 (Феденко 534)

Напишите параметрические уравнения гиперболического и параболического цилиндров.

Для гиперболического цилиндра:

Направляющая: $\vec{\rho}=\left\{\frac{a}{2}\left(u+\frac{1}{u}\right), \frac{b}{2}\left(u-\frac{1}{u}\right),0\right\}$,

Образующая: $\vec{\mu}=\{0,0,1\}$,
Уравнение:
\begin{equation*}
\vec{R}=\vec{\rho}(u)+v\vec{e}.
\end{equation*}
\begin{equation*}
\left\{
\begin{aligned}
&x=a\,\mbox{ch}\,u, \\
&y=b\,\mbox{sh}\,u,\\
&z=v.
\end{aligned}
\right.
\end{equation*}

Для параболического цилиндра — самостоятельно.

Задание 4 (Феденко 541)

Задана точка $M(a,b,c)$ и линия $L$:
\begin{equation*}
x=f(u), \,\, y=\varphi(u), \,\, z=\psi(u).
\end{equation*}
Напишите в параметрическом и неявном виде уравнения конуса с вершиной в точке $M$ и с направляющей линией $L$.

Коническая поверхность:

Вершина в точке $M(a,b,c)$,

Направляющая: $\vec{\rho}=\{f(u), \varphi(u), \psi(u)\}$,

Образующая: $\vec{\mu}=\vec{\rho}(u)-\vec{\rho}_0=\{f(u)-a, \varphi(u)-b, \psi(u)-c\}$.
\begin{equation*}
\vec{R}=\vec{\rho}_0+v(\vec{\rho}(u)-\vec{\rho}_0).
\end{equation*}
\begin{equation*}
\left\{
\begin{aligned}
&x=a+v\left(f(u)-a\right), \\
&y=b+v\left(\varphi(u)-b\right),\\
&z=c+v\left(\psi(u)-c\right).
\end{aligned}
\right.
\end{equation*}

Задание 5

Составьте параметрическое и неявное уравнения конуса, образуемого прямыми, проходящими через точку $M(1,1,1)$ и пересекающими эллипс:
\begin{equation*}
x=a\,\mbox{cos}\,u, \,\, y=b\,\mbox{sin}\,u, \,\, z=0.
\end{equation*}

Коническая поверхность:

Вершина в точке $M(1,1,1)$,

Направляющая: $\vec{\rho}=\{a\,\mbox{cos}\,u, b\,\mbox{sin}\,u, 0\}$,

Образующая: $\vec{\mu}=\vec{\rho}(u)-\vec{\rho}_0=\{a\,\mbox{cos}\,u-1, b\,\mbox{sin}\,u-1, -1\}$.
\begin{equation*}
\vec{R}=\vec{\rho}_0+v(\vec{\rho}(u)-\vec{\rho}_0).
\end{equation*}
\begin{equation*}
\left\{
\begin{aligned}
&x=1+v\left(a\,\mbox{cos}\,u-1\right), \\
&y=1+v\left(b\,\mbox{sin}\,u-1\right),\\
&z=1-v.
\end{aligned}
\right.
\end{equation*}

Неявное уравнение:
\begin{equation*}
\left(\frac{x-z}{a}\right)^2+\left(\frac{y-z}{b}\right)^2=(1-z)^2.
\end{equation*}

Задание 6 (Феденко 529)

Напишите уравнение тора, который получается при вращении окружности
\begin{equation*}
x=a+b\,\mbox{cos}\,u, \,\, y=0 , \,\, z=b\,\mbox{sin}\,u \,\, (b<a)
\end{equation*}
вокруг оси $Oz$.

\begin{equation*}
x=(a+b\,\mbox{cos}\,u)\,\mbox{cos}\,v, \,\, y= (a+b\,\mbox{cos}\,u)\,\mbox{sin}\,v, b\, \,\, z=\mbox{sin}\,u.
\end{equation*}

Приложения

Промышленное котельное производство

Изделие котельное (производство: Olivier Roger). Линейчатые поверхности на фото выглядят серыми.

Котел представляет собой листовой металл (листовой металл). При формовании листов используются два основных метода: прокатка (или гибка) и гибка .

Катание дает поверхности вращения, части конусов или цилиндров. Следовательно, они представляют собой линейчатые поверхности.

Складывание позволяет приближаться к поверхностям, ограниченным многогранниками, причем складки / ребра соответствуют образующим поверхности, к которой нужно приблизиться.

Серые части на прилагаемом фото – линейчатые поверхности котельной.

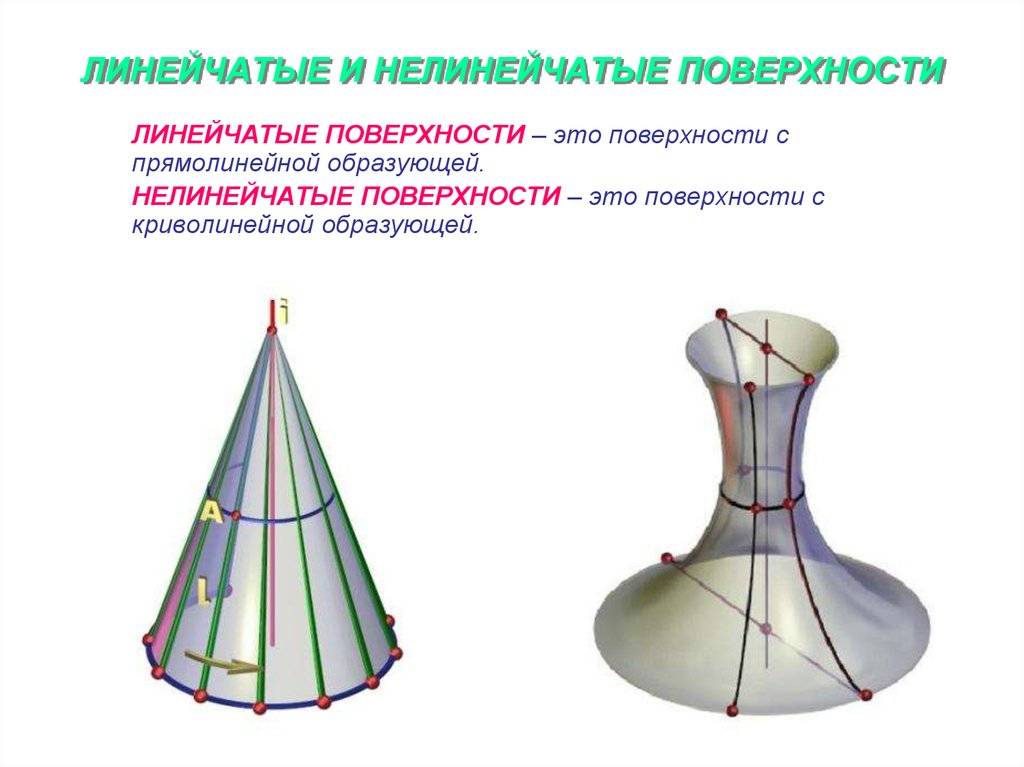
Линейчатые поверхности

Одним из объектов трехмерного пространства являются поверхности. Это непрерывное, бесконечное множество точек, которые имеют определенную, строго установленную, зависимость между координатами. Основными инструментами трехмерного моделирования служат различные способы их отражения.

В инженерной графике, начертательной геометрии есть метод, когда поверхность рассматривается как комплекс последовательных расположений линии, которая, подчиняясь определенному закону, перемещается в пространстве. Это кинематический способ, благодаря которому образуются геометрические объекты. Примером выступают технологические процессы, связанные с обработкой материала режущим инструментом. Плоскость получаемого изделия рассматривается как множество линий, эквивалентных (конгруэнтных) форме профиля резца режущего инструмента.

Для описания процесса образования используются два основных термина:

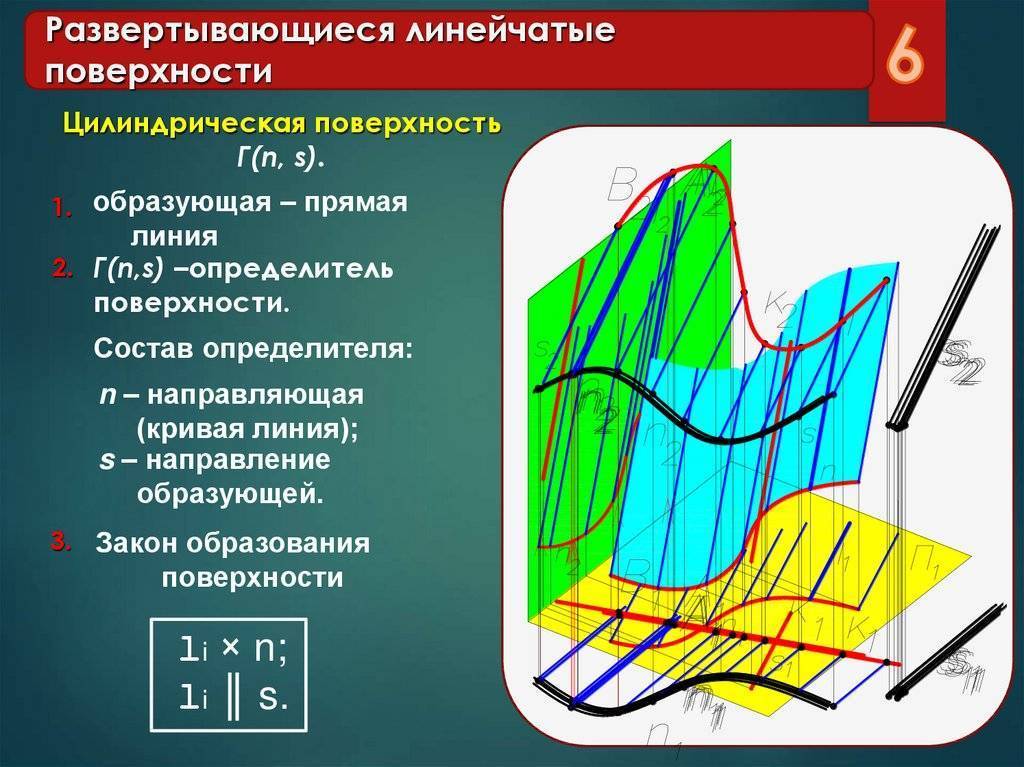
1. Образующая – это подвижная линия. Она, перемещаясь, может иметь постоянную форму. Если это кривая — получается нелинейчатая поверхность. Она относится к I классу. Когда образующая представлена прямой, это ведет к формированию линейчатой поверхности (II класс).
2. Направляющая – это неподвижная линия или плоскость, по ней движется образующая. Однозначно определить рассматриваемый объект возможно тремя линиями, задающими траекторию движения. Но, должно выполняться требование: две из трех линий задаются произвольно, третья – должна быть внутри конгруэнции, которая определяется уже выбранными двумя.

Такое перемещение не является хаотичным, оно подчиняется определенному закону. Законом может выступать перемещение вдоль неподвижных линий. Иными словами, образующая все время занимает конкретное установленное положение.

Определены следующие два вида линейчатых поверхностей:

• развертывающаяся;
• неразвертывающаяся (косая).

В пределах класса эти объекты, образованные перемещением прямой линии, подразделяются на:

1. Группы. Классификация на группы зависит от внешних условий движения образующей, то есть от количества направляющих.
2. Виды. Деление на виды по каждой группе определяется внутренними характеристиками движения – формой и относительным положением траекторий, по которым движется прямая.

Их образование может происходить вращением или поступательным передвижением образующей прямой. Цилиндры, конусы – примеры геометрических тел, образованных пересечением линейчатой поверхности вращения с областью, называемой основанием. Гранные объекты формируются поступательным передвижением образующей вдоль ломанных траекторий. Так образуются призмы и пирамиды.

Презентация на тему: ” Линейчатые поверхности Образование поверхностей. Линейчатой поверхностью называется поверхность, образованная перемещением прямолинейной образующей по.” — Транскрипт:

1

Линейчатые поверхности Образование поверхностей

2

Линейчатой поверхностью называется поверхность, образованная перемещением прямолинейной образующей по одной или более направляющим

3

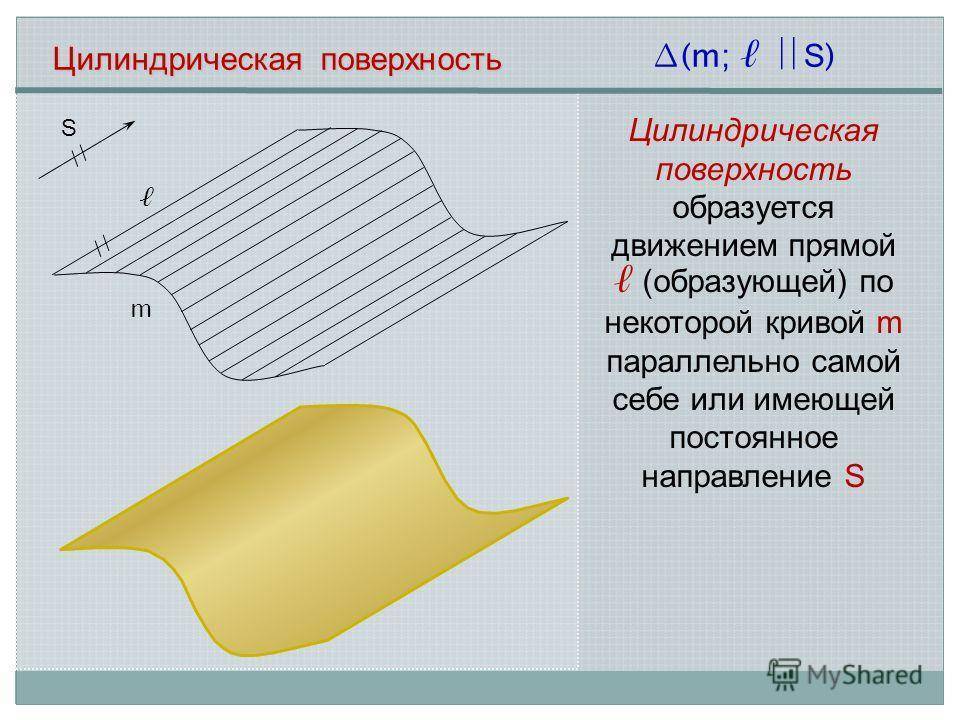
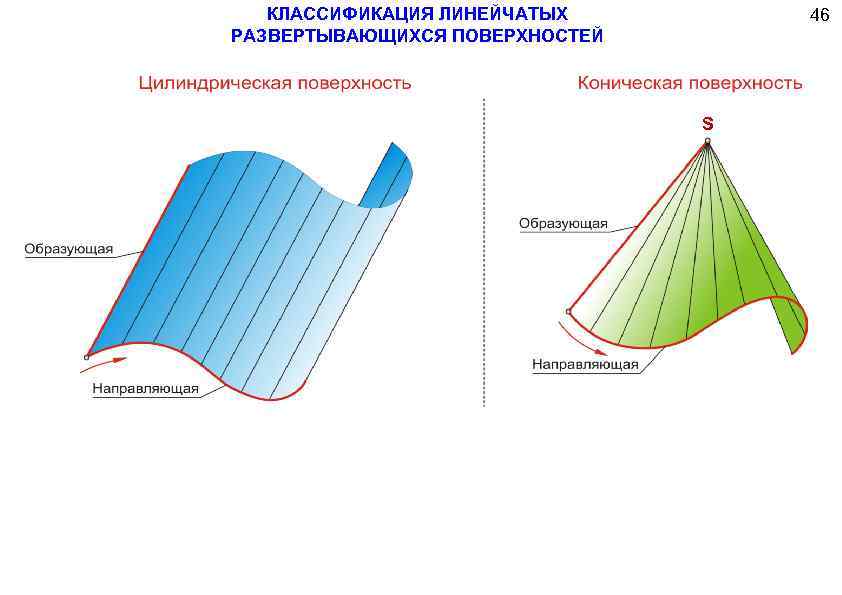
Цилиндрическая поверхность m (m; S ) S // Цилиндрическая поверхность образуется движением прямой (образующей) по некоторой кривой m параллельно самой себе или имеющей постоянное направление S

4

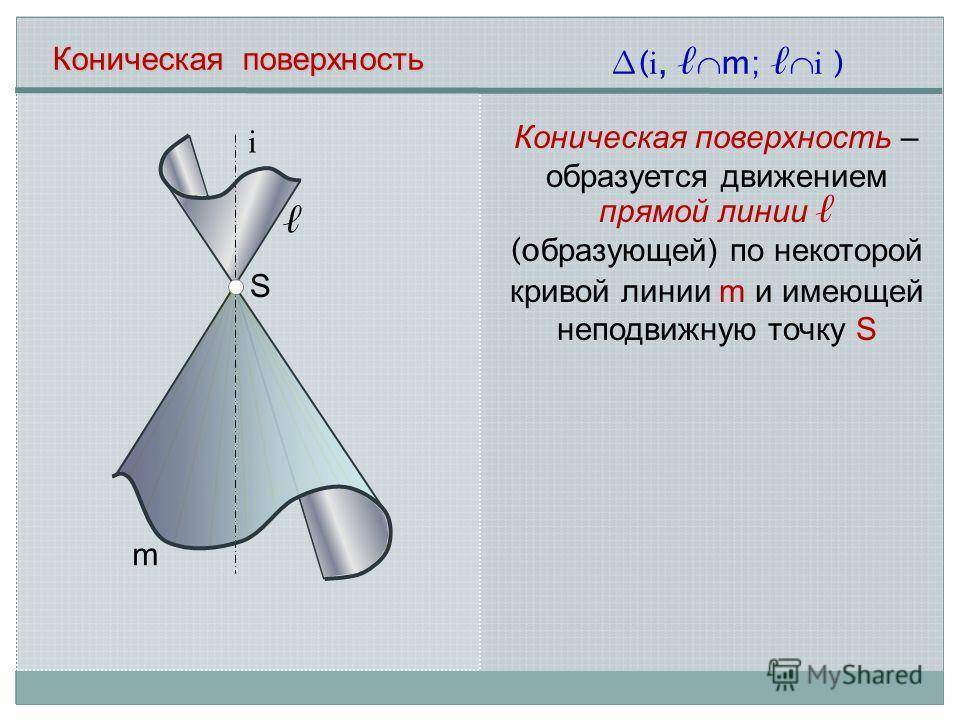
i m ( i, m; i ) Коническая поверхность Коническая поверхность – образуется движением прямой линии (о бразующей) по некоторой кривой линии m и имеющей неподвижную точку S S

5

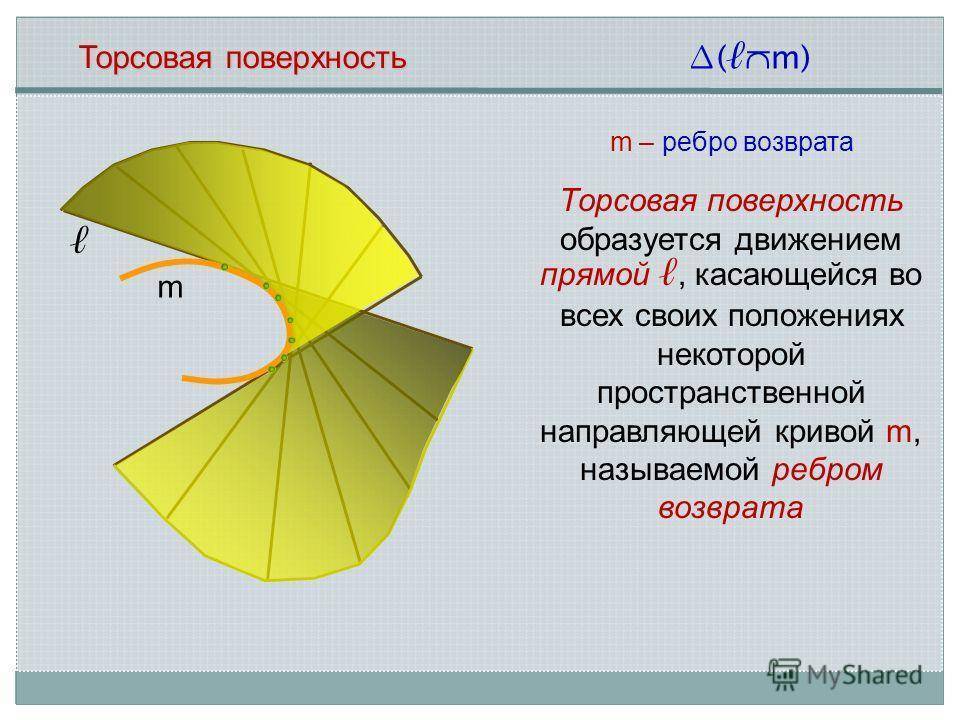
Торсовая поверхность m m – ребро возврата ( m) Торсовая поверхность образуется движением прямой, касающейся во всех своих положениях некоторой пространственной направляющей кривой m, называемой ребром возврата

6

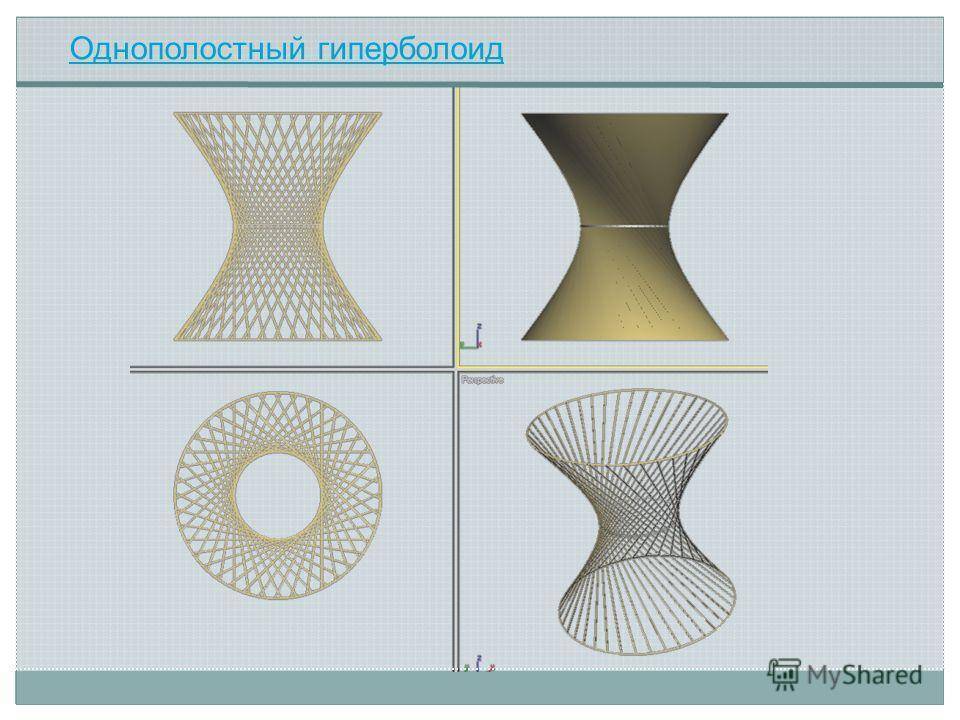
Однополостный гиперболоид

7

Многогранные поверхности – это поверхности, образованные частями (отсеками) пересекающихся плоскостей Многогранником называется тело, ограниченное многогранной поверхностью, состоящей из плоских многоугольников Отсеки плоскостей называются гранями, а линии их пересечения – ребрами Точки пересечения ребер называются вершинами

8

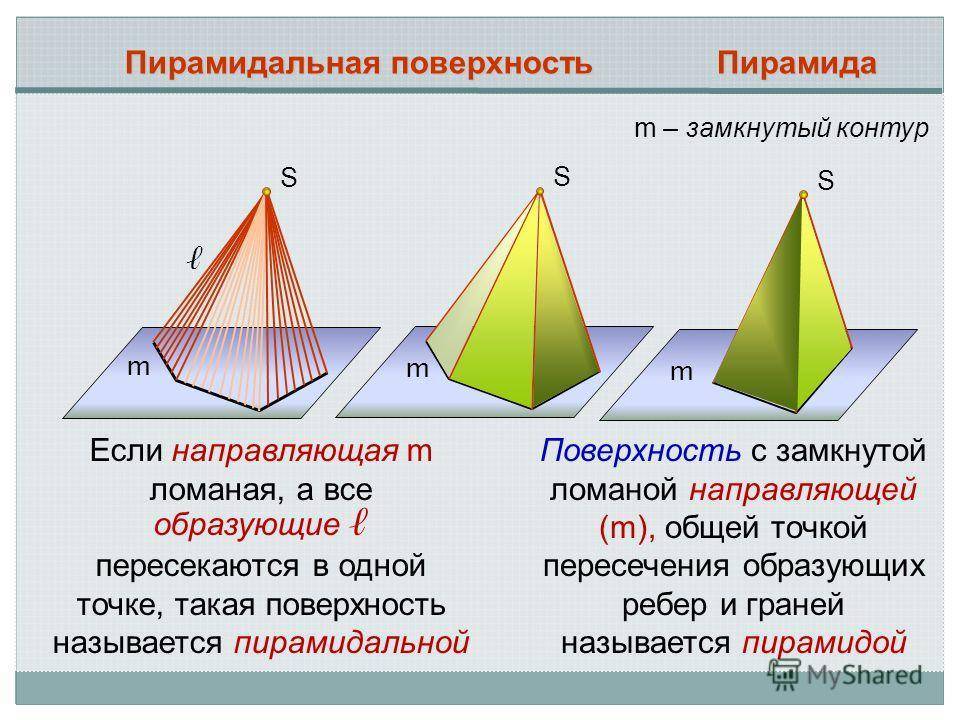
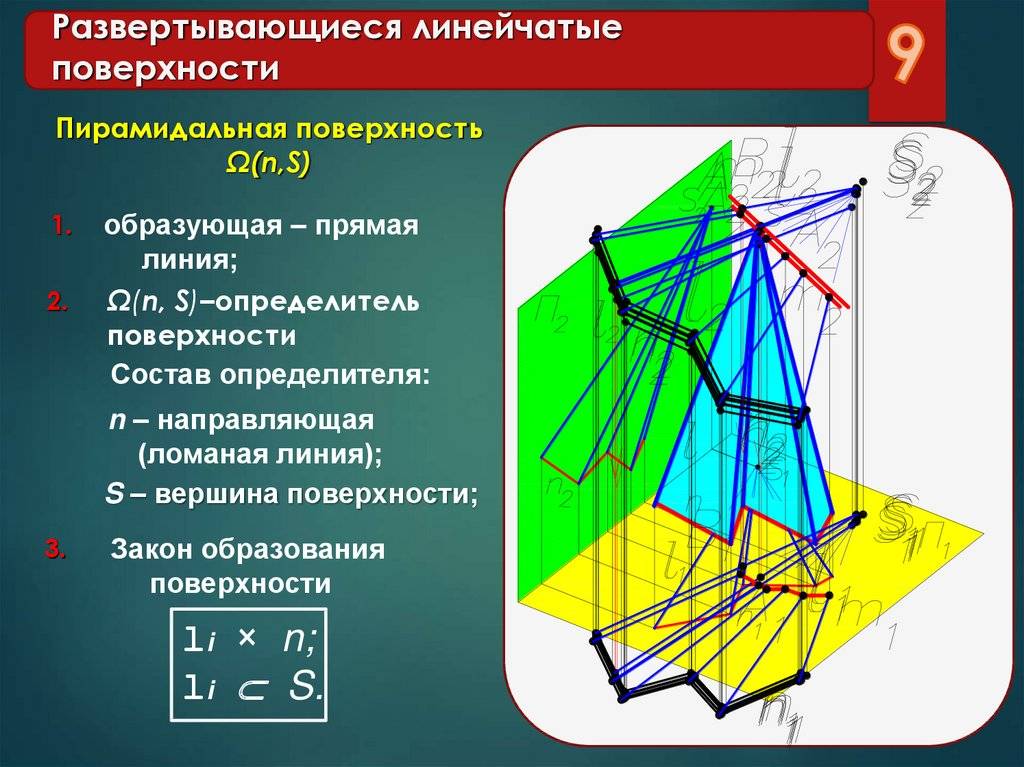
S m S m Пирамидальная поверхность S m Пирамида m – замкнутый контур Если направляющая m ломаная, а все образующие пересекаются в одной точке, такая поверхность называется пирамидальной Поверхность с замкнутой ломаной направляющей (m), общей точкой пересечения образующих ребер и граней называется пирамидой

9

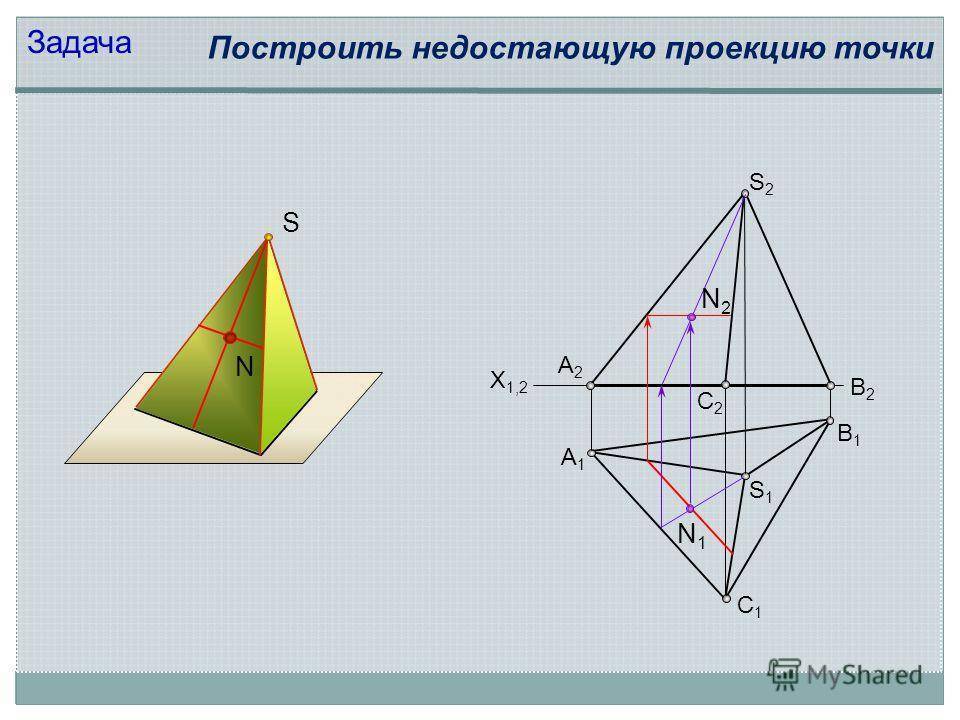
Принадлежность точки поверхности

10

S А1А1 С1С1 В1В1 S2S2 X 1,2 S1S1 А2А2 С2С2 В2В2 Задача Построить недостающую проекцию точки N N2N2 N1N1

11

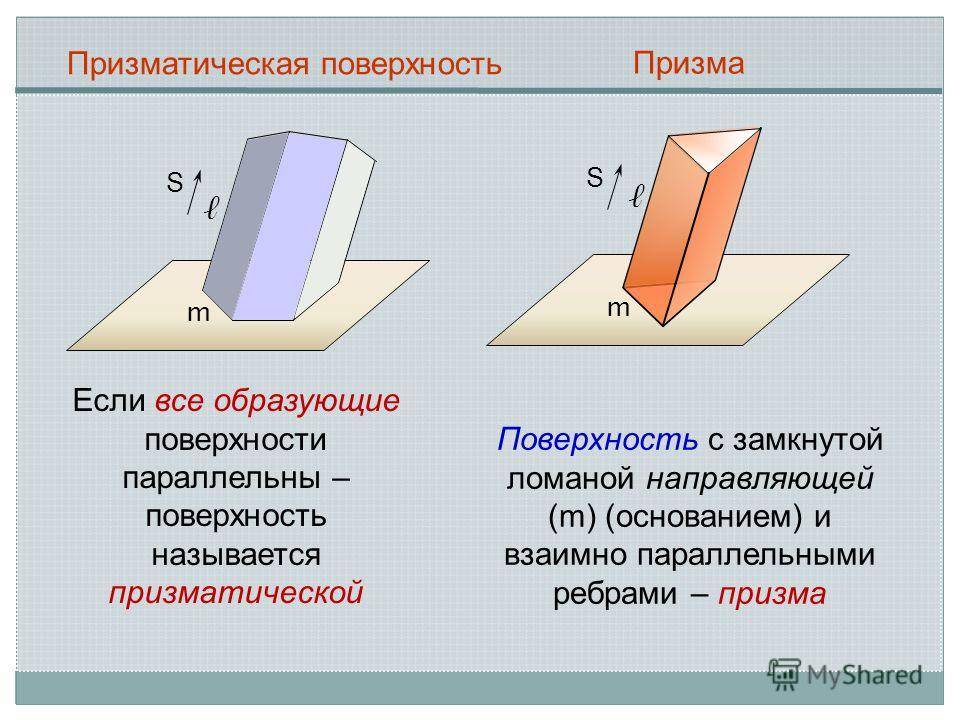
m S Призматическая поверхность m S Призма Если все образующие поверхности параллельны – поверхность называется призматической Поверхность с замкнутой ломаной направляющей (m) (основанием) и взаимно параллельными ребрами – призма

12

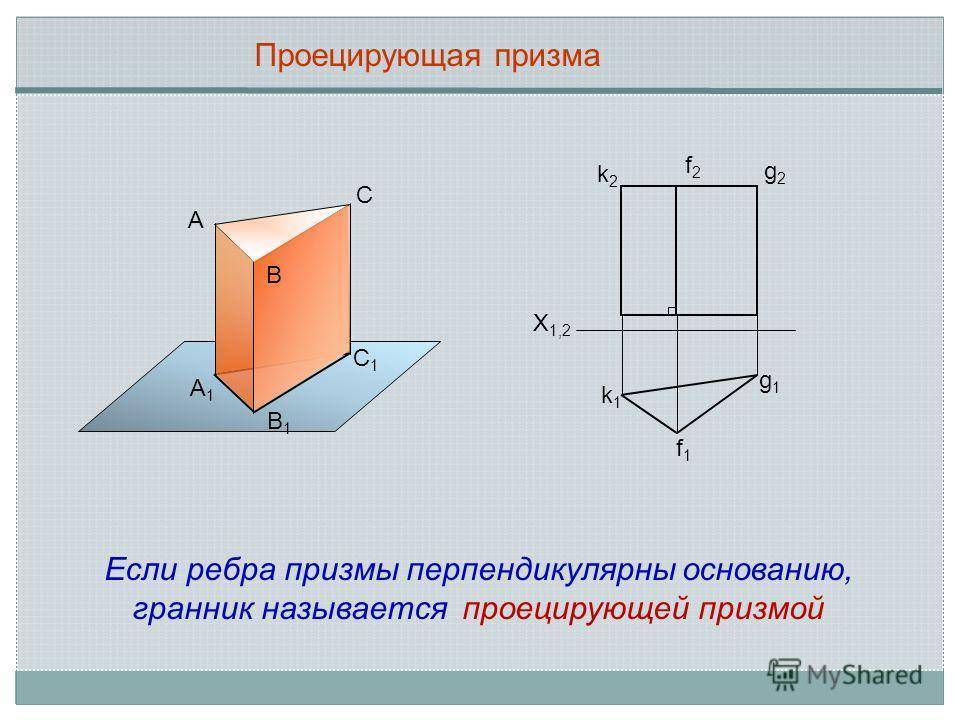
Проецирующая призма А В С С1С1 В1В1 А1А1 k2k2 k1k1 f1f1 g1g1 g2g2 f2f2 X 1,2 Если ребра призмы перпендикулярны основанию, гранник называется проецирующей призмой

13

Поверхности Каталана

14

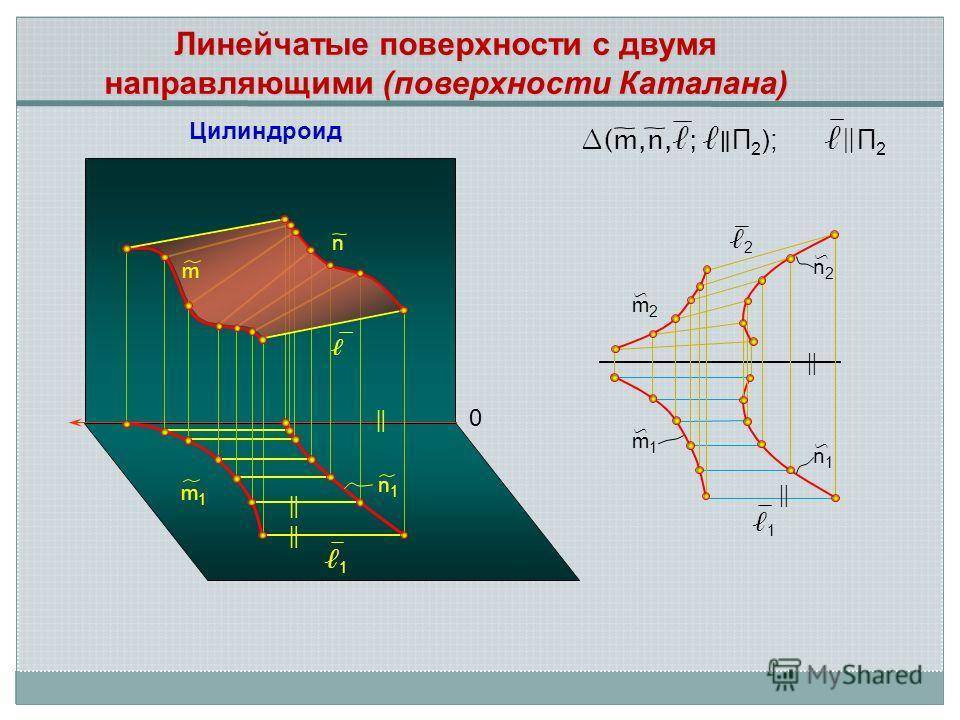
0 m1m1 n1n1 1 1 n m n1n1 m1m1 2 m2m2 n2n2 Линейчатые поверхности с двумя направляющими (поверхности Каталана) П 2 (m,n,; П 2 ); Цилиндроид

15

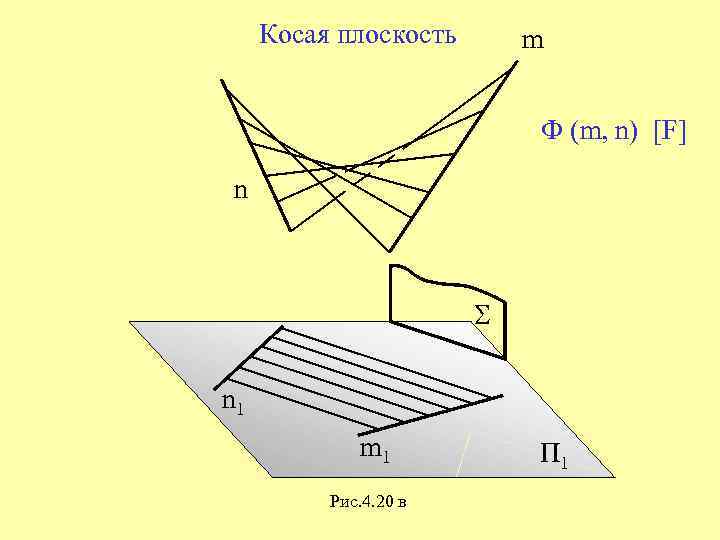
Поверхность с плоскостью параллелизма и двумя скрещивающимися направляющими называется гиперболическим параболоидом, или косой плоскостью Гипар

16

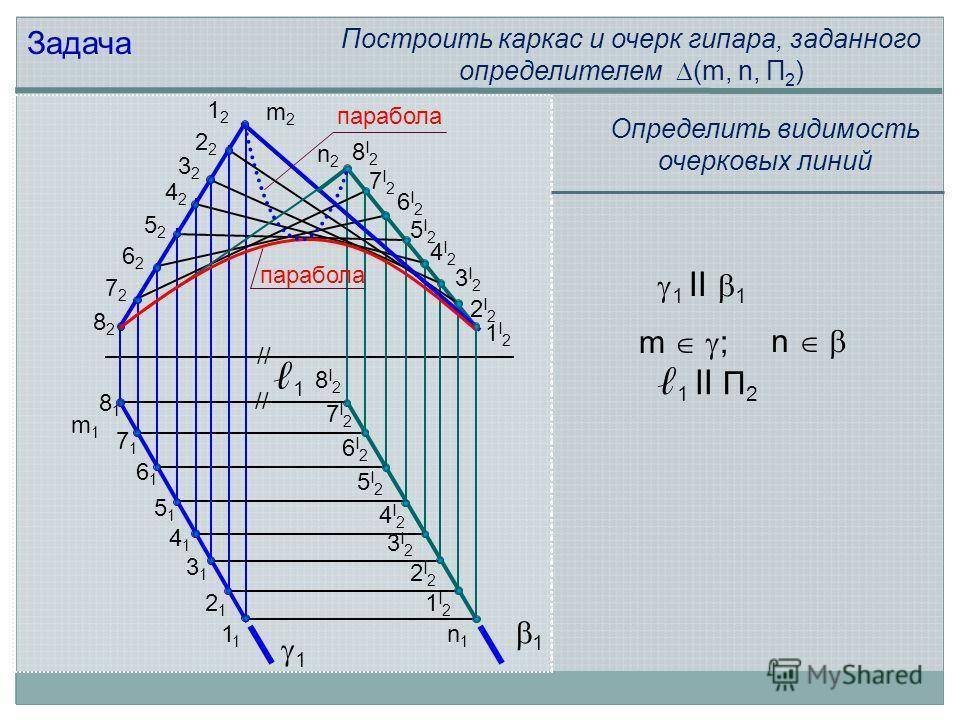
m2m2 n2n2 n1n1 m1m1 Задача Построить каркас и очерк гипара, заданного определителем (m, n, П 2 ) I21I2 2I22I2 3I23I2 4I24I2 5I25I2 6I26I2 7I27I2 8I28I I21I2 2I22I2 3I23I2 4I24I2 5I25I2 6I26I2 7I27I2 8I28I2 // парабола ll 1 n m ; 1 1 ll П 2 Определить видимость очерковых линий

17

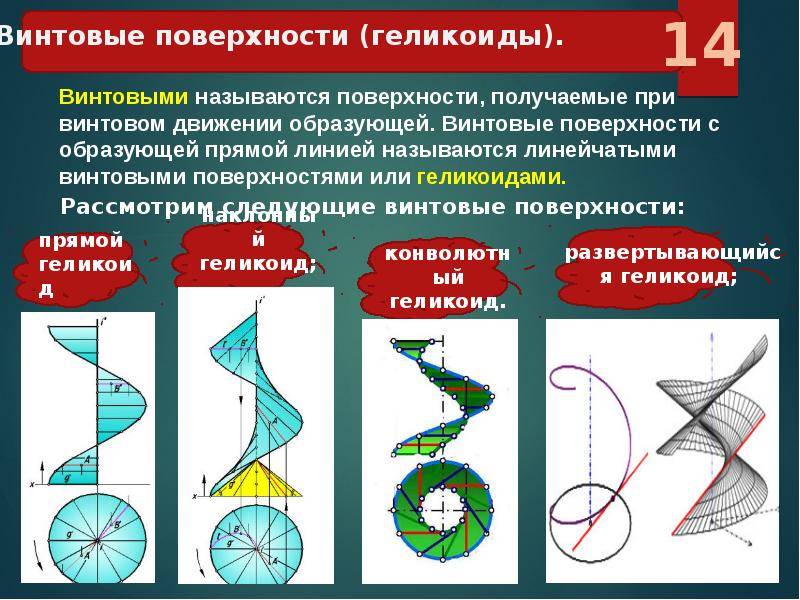
Винтовой поверхностью называют поверхность, образованную винтовым движением образующей Винтовым движением называют движение, при котором каждая точка А образующей вращается вокруг неподвижной оси i и одновременно перемещается поступательно вдоль этой оси Винтовая поверхность

18

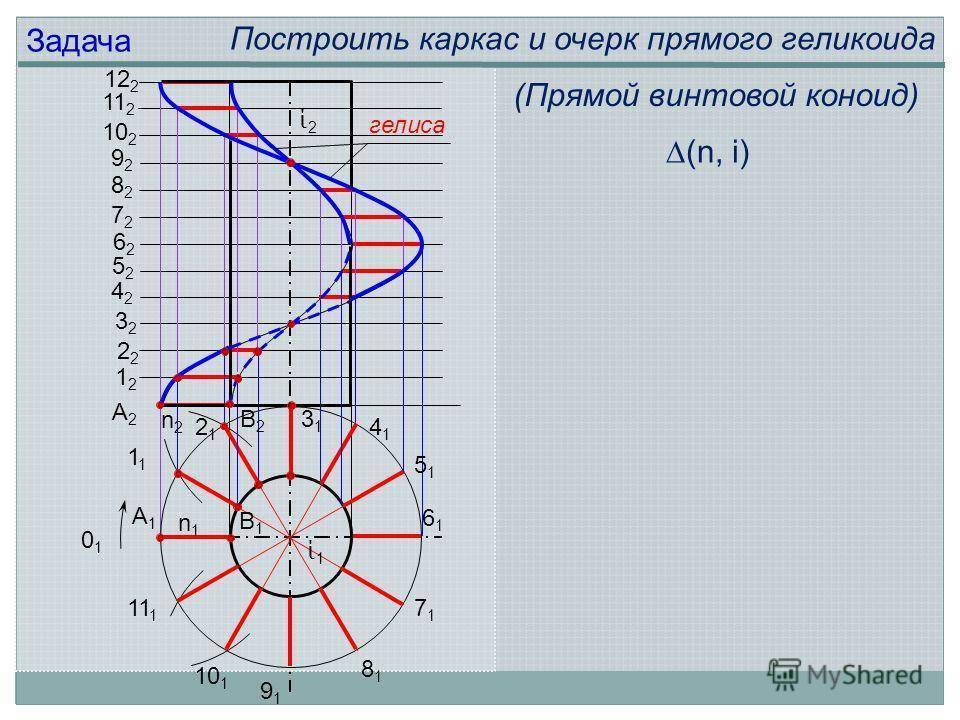
n2n2 n1n1 гелиса А1А1 В1В1 ί1ί1 ί2ί2 Задача Построить каркас и очерк прямого геликоида А2А2 В2В (Прямой винтовой коноид) (n, i)

19

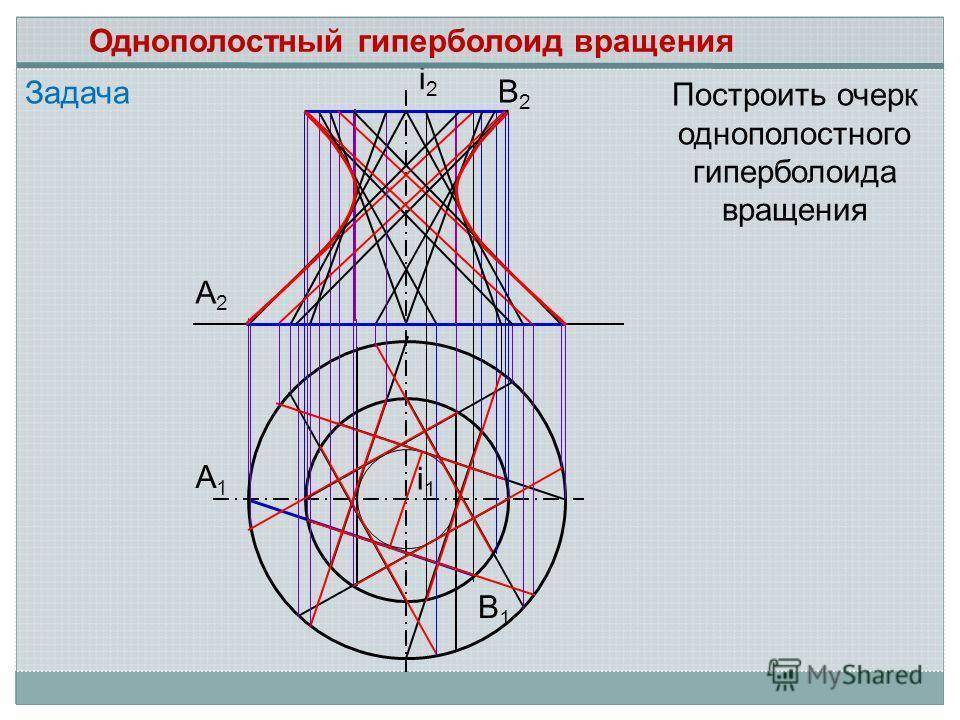
Задача А2А2 А1А1 В1В1 В2В2 i2i2 i1i1 Построить очерк однополостного гиперболоида вращения Однополостный гиперболоид вращения

7.10. Пересечение цилиндра плоскостью

Пусть плоскость сечения γ – фронтально-проецирующая (Рисунок 7.15).

1. Если плоскость сечения γ параллельна оси цилиндра, то она пересекает цилиндр по четырехугольнику.
2. Если плоскость сечения γ перпендикулярна оси цилиндра, то она пересекает цилиндр по окружности.
3. Если плоскость сечения γ не параллельна и не перпендикулярна оси цилиндра в сечении эллипс.

Рассмотрим алгоритм построения сечения – эллипс (Рисунок 7.15):

Рисунок 7.15 – пересечение цилиндра плоскостью

1. Находим и строим характерные точки (точки, не требующие дополнительных построений) – в нашем случае, точки принадлежащие крайним образующим – 1, 3, 5, 7. Одновременно с этим, данные точки определяют величину большой и малой оси эллипса.
2. Для построения участка эллипса необходимо построить не менее 5-ти точек (так как лекальная кривая второго порядка определяется как минимум пятью точками). Для построения точек 2, 4, 6, 8 возьмем на π₁ произвольно расположенные образующие цилиндра, которые проецируются на данную плоскость проекции в точки.
3. Построим вторые проекции данных образующих. Из точек пересечения вторых проекций образующих с проекцией плоскости сечения γ проводим линии связи к π₃. Для построения третьей проекции, например, точки 6 измеряем расстояние Δ₁ и откладываем его по соответствующей линии связи на π₃. Симметрично ей, относительно оси вращения, строим точку 4. Аналогично строятся другие точки.

Параметрическое представление

Пример линейчатой ​​поверхности.

Мы можем описать линейчатую поверхность S , рассматривая его как в виде семейства линий D ( U ) в зависимости от параметра у обхода части I множества действительных чисел . Для этого достаточно , чтобы дать для каждого U в I точку P ( U ) и направляющий вектор из D ( ¯u ). Тогда мы получим параметрическое представление поверхности S  : V(ты)→{\ displaystyle {\ overrightarrow {V (u)}}}м∈S⟺∃ты∈я∃v∈рM(ты,v)знак равноп(ты)+vV(ты)→.{\ Displaystyle м \ в S \ iff \ существует и \ в я \ четырехъядерный \ существует v \ в \ mathbb {R} \ четырехъядерный M (u, v) = P (u) + v \, {\ overrightarrow {V ( u)}}.}

Дуга установлено с помощью называется директрисой кривой из S . ты∈я↦п(ты)∈р3{\ Displaystyle и \ ин I \ mapsto P (u) \ in \ mathbb {R} ^ {3}}

В примере напротив мы взяли п(ты)знак равно(ты,-ты2,ты3)етV(ты)→знак равно(-ты2,1,ты).{\ Displaystyle P (u) = (u, -u ^ {2}, u ^ {3}) \ quad {\ rm {et}} \ quad {\ overrightarrow {V (u)}} = (- u ^ {2}, 1, u).}

Развертывающиеся поверхности

Эти объекты важны для листопрокатного производства, текстильной промышленности, авиа- и автомобилестроения. Представление о них основывается на допущении, что они обладают гибкостью, но они нерастяжимы и несжимаемы. Под развертывающимися понимают области, которые, изгибая, можно совмещать с плоскостью без порывов, перегибов и складок. Таким образом получается развертка. Это свойство характерно для многогранных объектов и объектов, которые имеют ребра возврата.

Ребро возврата – это направляющая кривая в пространстве, которую касается прямая при передвижении. В системе отсчета развертывающаяся линейчатая поверхность определяется ребром возврата. Указанными характеристиками обладают: торс, а также его частные случаи: объекты, имеющие форму конуса, цилиндра, призмы, пирамиды.

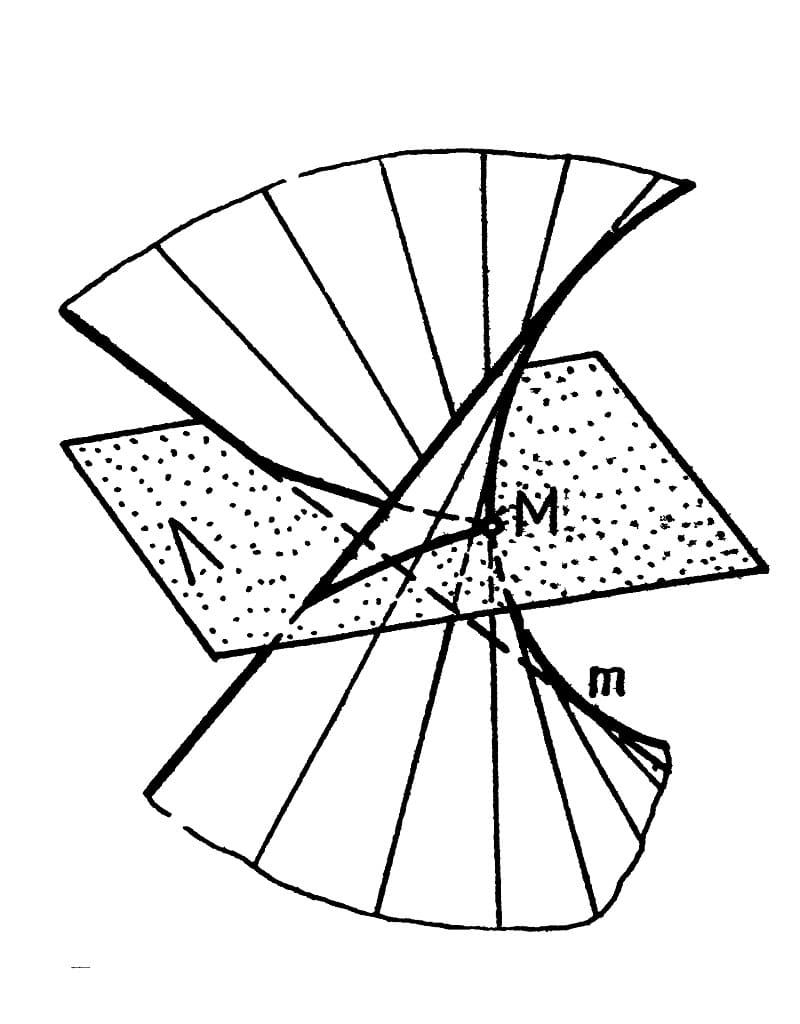
Торс

Торсы используются при проектировании деталей и узлов в машиностроении. Образование линейчатых поверхностей, имеющих вид торса, происходит при передвижении образующей, которая во всех позициях проходит по касательной относительно ребра возврата. Оно, совместно с движущейся прямой, определяет торс в пространстве. Этот геометрический объект составляют две полости, граничащие по ребру возврата.

Цилиндрическая

Это особый вид торса. При этом ребро возврата переродилось в несобственную точку, удаленную на бесконечное расстояние. Построенная прямая образующая движется параллельно самой себе по установленной кривой. Чтобы определить цилиндрическую поверхность надо задаться: вектором перемещения и криволинейной траекторией движения.

Коническая

В ней ребро возврата преобразовалось в собственную точку, через которую, по определенной кривой, проходит образующая. Эта точка служит вершиной конуса. Такой объект может складываться из двух полостей. Для его определения задаются указанными точкой и кривой.

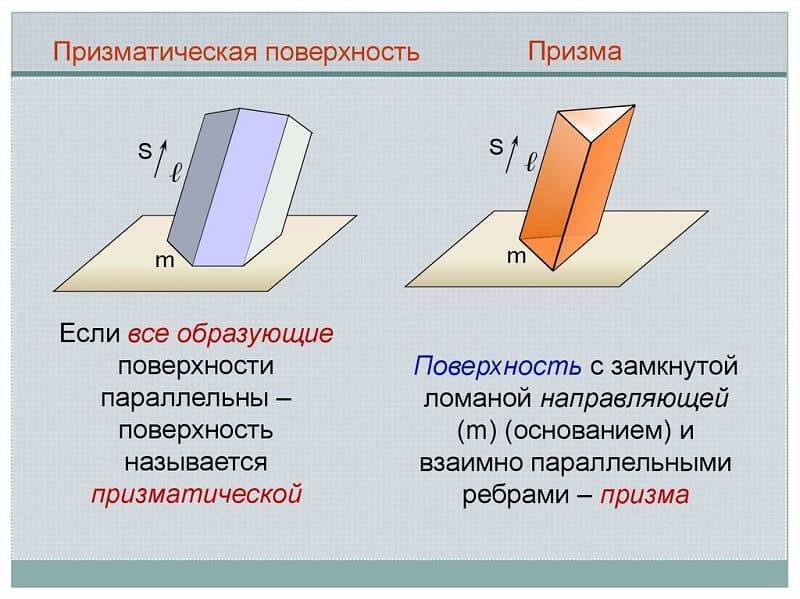
Призматическая и пирамидальная

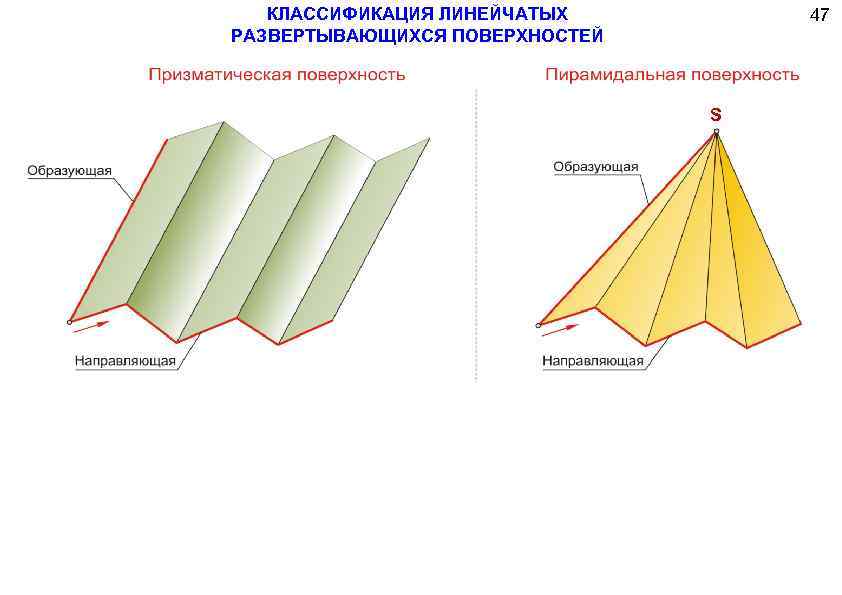
Призматическая отличается от цилиндрической тем, что движение прямой происходит не по кривой траектории, а по ломанной. Ребро возврата преобразовалось в несобственную точку, которая находится на бесконечном расстоянии.

Пирамидальная и конусная различаются формой траектории движения прямой. У конусной — траектория движения криволинейная, у пирамидальной – ломанная.

У перечисленных видов две смежные прямые могут:

• пересекаться (торс, коническая, пирамидальная);
• быть параллельными (цилиндрическая, призматическая).

Чтобы получить уравнение поверхности развертывающейся надо решить систему двух уравнений:

1. уравнения образующей.
2. уравнения направляющей.

Рассмотренные объекты могут быть замкнутыми, если траектория имеет форму окружности или замкнутого многоугольника.

1.6. ВЗАИМНОЕ ПОЛОЖЕНИ ЛИНИИ И ПОВЕРХНОСТИ

Различают четыре возможных варианта взаимного положения линии и поверхности:

–  линия и поверхность не имеют общих точек;

–  линия касается поверхности;

–  линия принадлежит поверхности;

–  линия пересекает поверхность.

Первый вариант не рассматривают, т. к. он не имеет практического применения. Способ построения линий, принадлежащих поверхности основан на использовании ее каркаса и рассмотрен на примерах разработки комплексных чертежей поверхностей (рис. 1.54 и 1.57).

1.6.1. Построение касательной к поверхности

Задачу на построение касательной к поверхности сводят к построению касательной к линии, которая принадлежит поверхности и проходит через заданную точку.

Из за большого объема этот материал размещен на нескольких страницах:1 2 3 4 5 6 7 8 9 10 11 12 13 14