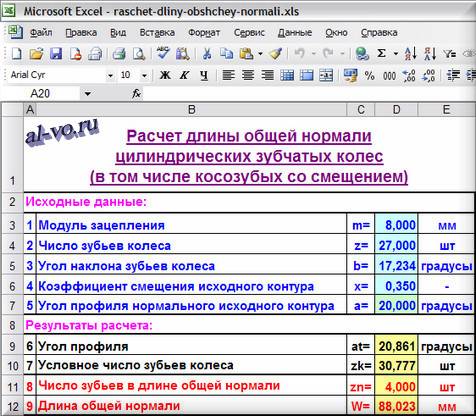
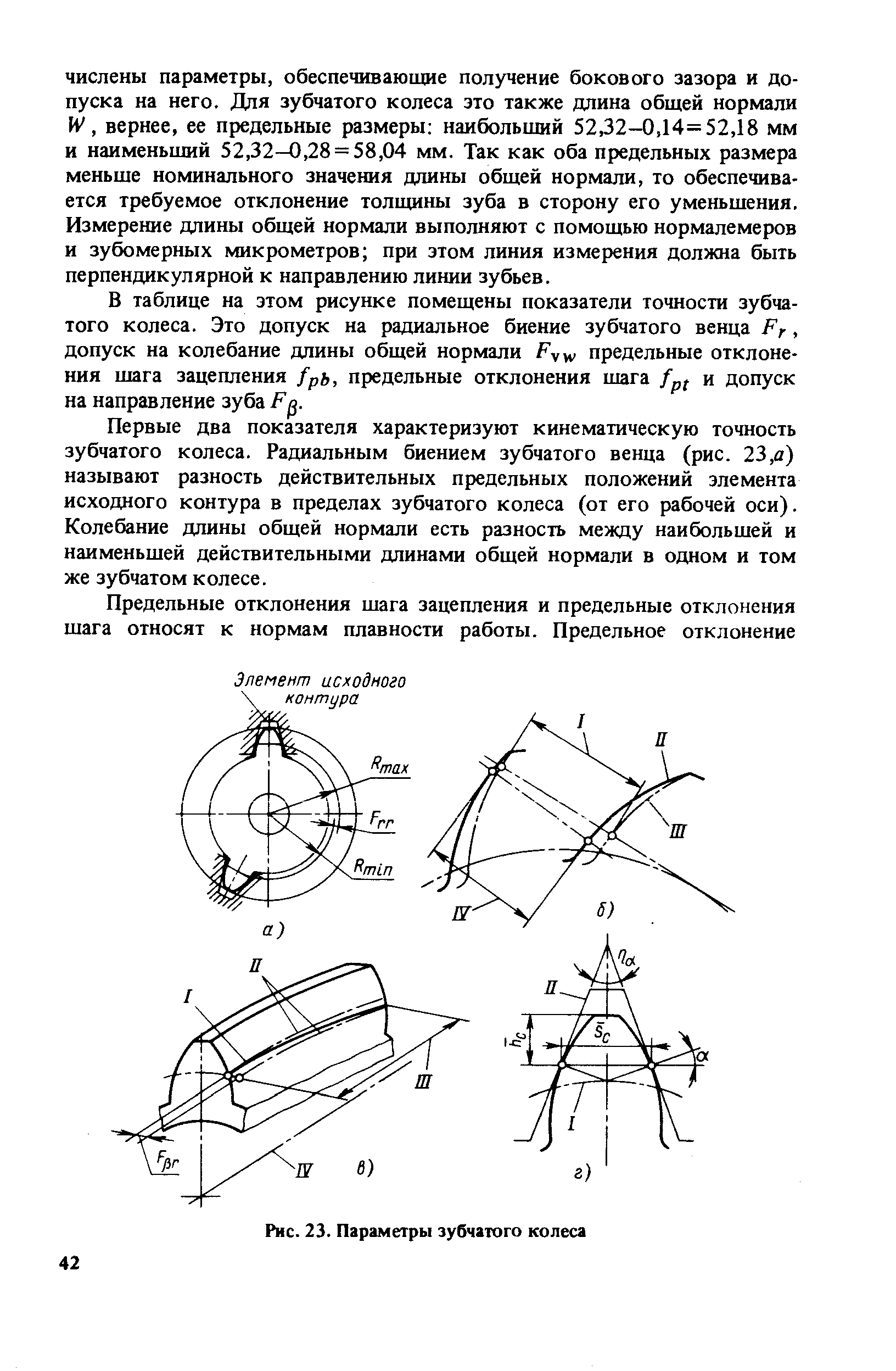
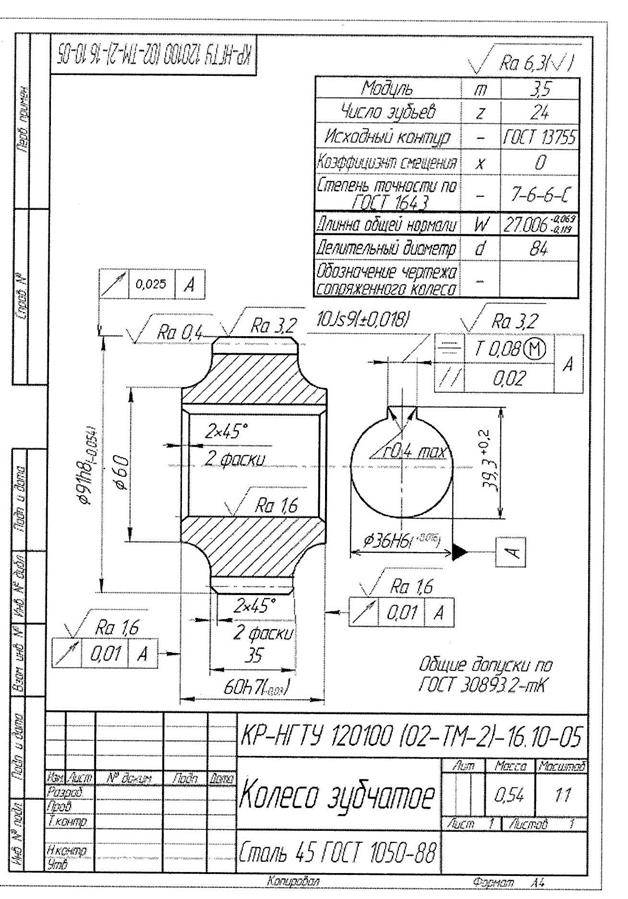
Геометрический расчет элементов цилиндрической зубчатой передачи
Исходные данные для расчета:
- Модуль m = 4 мм;
- Число зубьев шестерни Z1 = 18;
- Число зубьев колеса Z2 = 30;
- Диаметр вала (ведущий) DB1 = 22 мм;
- Тип шпонки – Призматическая;
- Число шлицев Z – 8;
- Внутренний диаметр шлицев d = 22 мм;
- Диаметр вала (ведомый) DB2 = 30 мм;
- Ширина шлица b = 6 мм;
- Тип – D.
Результаты геометрического расчета цилиндрической зубчатой передачи
- Делительный диаметр шестерни d1=mz1=4×18=72 мм;
- Делительный диаметр колеса d2=mz2=4×30=120 мм;
- Высота головки зуба ha=m =4 мм;
- Высота ножки зуба hf=1,25m=1,25×4=5 мм;
- Высота зуба h=ha+hf=2,25m=2,25×4=9 мм;
- Диаметр вершин зубьев шестерни da1=d1+2ha1=72+2×4=80 мм;
- Диаметр впадин шестерни df1=d1-2hf=72-2×5=62 мм;
- Длина ступицы шестерни Lст1=1,5DB1=1,5×22=33 мм;
- Наружный диаметр ступицы шестерни Dст1=1,6DB1=1,6×22=35,2 мм;
- Диаметр вала шестерни D1=1,2×22=26,4 мм;
- Делительный диаметр колеса d2=mz2=4×30=120 мм;
- Диаметр вершин зубьев колеса da2=d2+2ha=120+2×4=128 мм;
- Диаметр впадин колеса df2=d2-2hf2=120-2×5=110 мм;
- Длина ступицы колеса Lст2=1,5DB2=1,5×30=45 мм;
- Наружный диаметр ступицы колеса Dст2=1,6DB2=1,6×30=48 мм;
- Диаметр вала колеса D2=1,2DB2=1,2×30=36 мм;
- Ширина зубчатого венца b=6m=6×4=24 мм;
- Толщина обода зубчатого венца δ1=2,25m=2,25×4=9 мм;
- Толщина диска δ2=1/3b=8 мм;
- Межосевое расстояние a=0,5(d1+d2)=0,5(72+120)=96 мм;
- Длина шлицев Lшл=(1,5. 2)Lст2=(1,5. 2)45=72 мм.
Что такое модуль зубчатого колеса
Современные шестерни далеко ушли от своих деревянных шестизубых предков, изготавливаемых механиками с помощью воображения и мерной веревочки. Конструкция передач намного усложнилась, тысячекратно возросли скорость вращения и усилия, передаваемые через такие передачи. В связи с этим усложнились и методы их конструирования. Каждую шестеренку характеризует несколько основных параметров
- диаметр;
- число зубьев;
- шаг;
- высота зубца;
- и некоторые другие.
Одним из самых универсальных характеристик является модуль зубчатого колеса. Существует для подвида — основной и торцевой.
В большинстве расчетов используется основной. Он рассчитывается применительно к делительной окружности и служит одним из важнейших параметров.
Для расчета этого параметра применяют следующие формулы:
m=t/π,
где t — шаг.
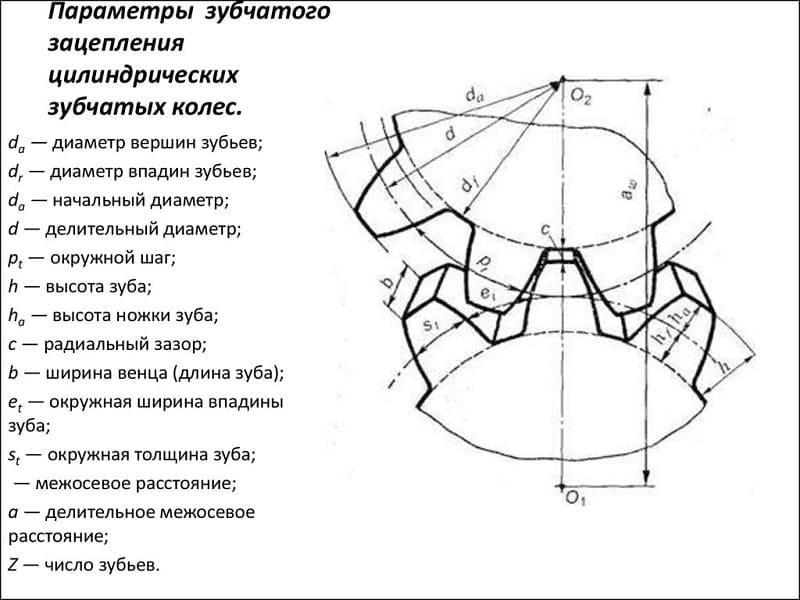
Параметры зубчатых колес
Модуль зубчатого колеса можно рассчитать и следующим образом:
m=h/2,25,
где h — высота зубца.
И, наконец,
m=De/(z+2),
где De — диаметр окружности выступов,а z — число зубьев.
Что же такое модуль шестерни?
это универсальная характеристика зубчатого колеса, связывающая воедино такие его важнейшие параметры, как шаг, высота зуба, число зубов и диаметр окружности выступов. Эта характеристика участвует во всех расчетах, связанных с конструированием систем передач.
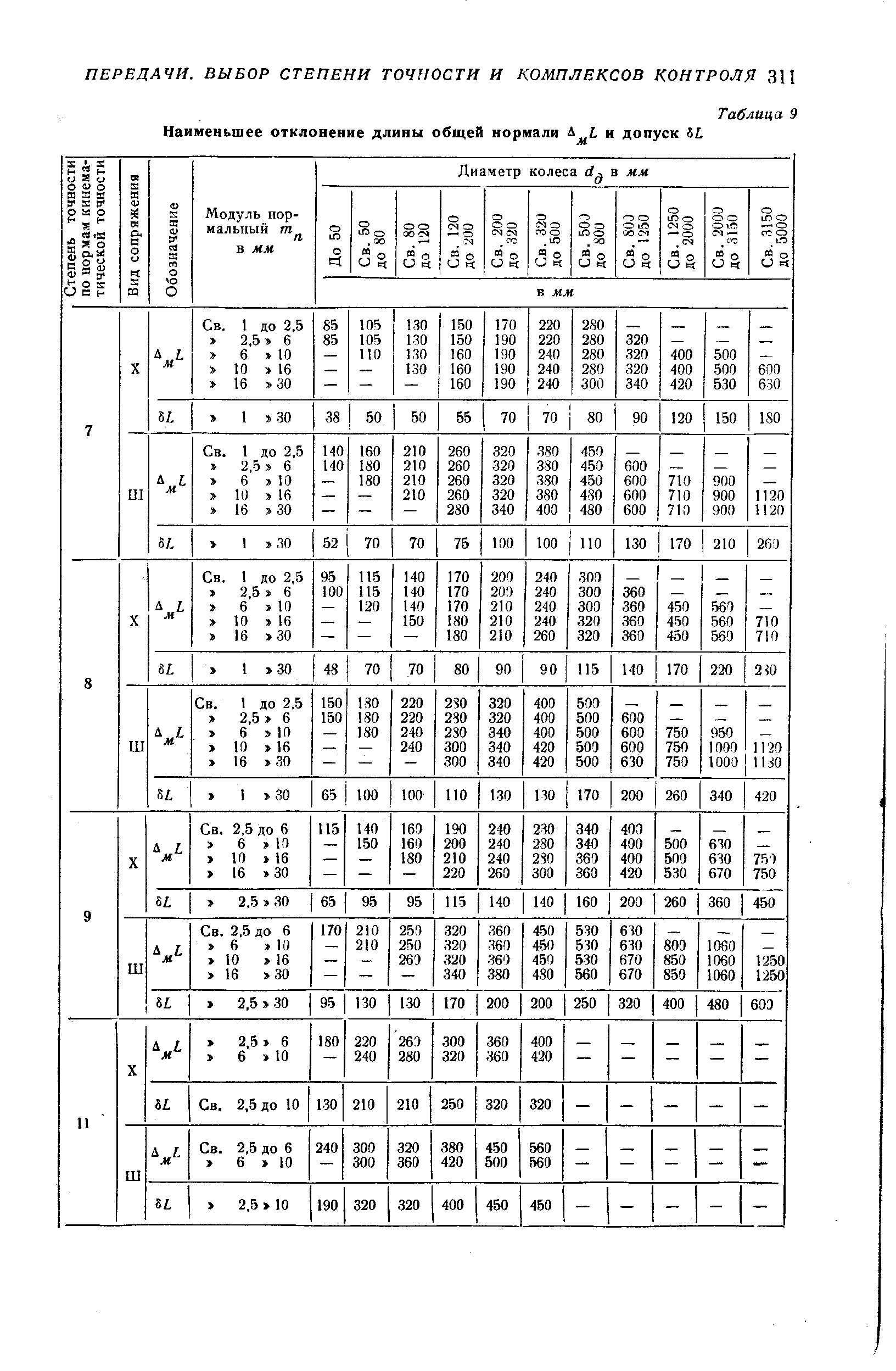
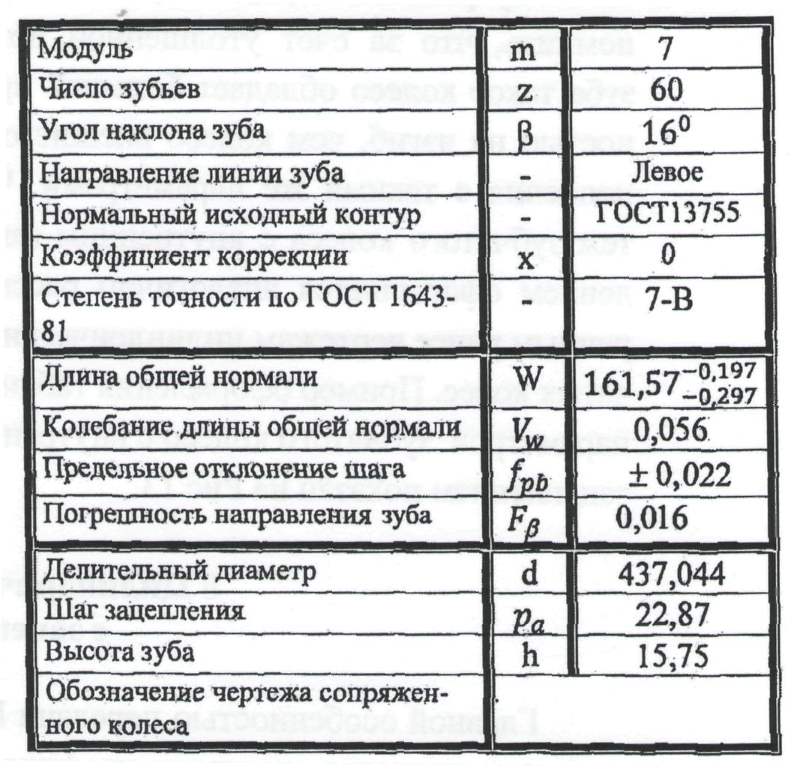
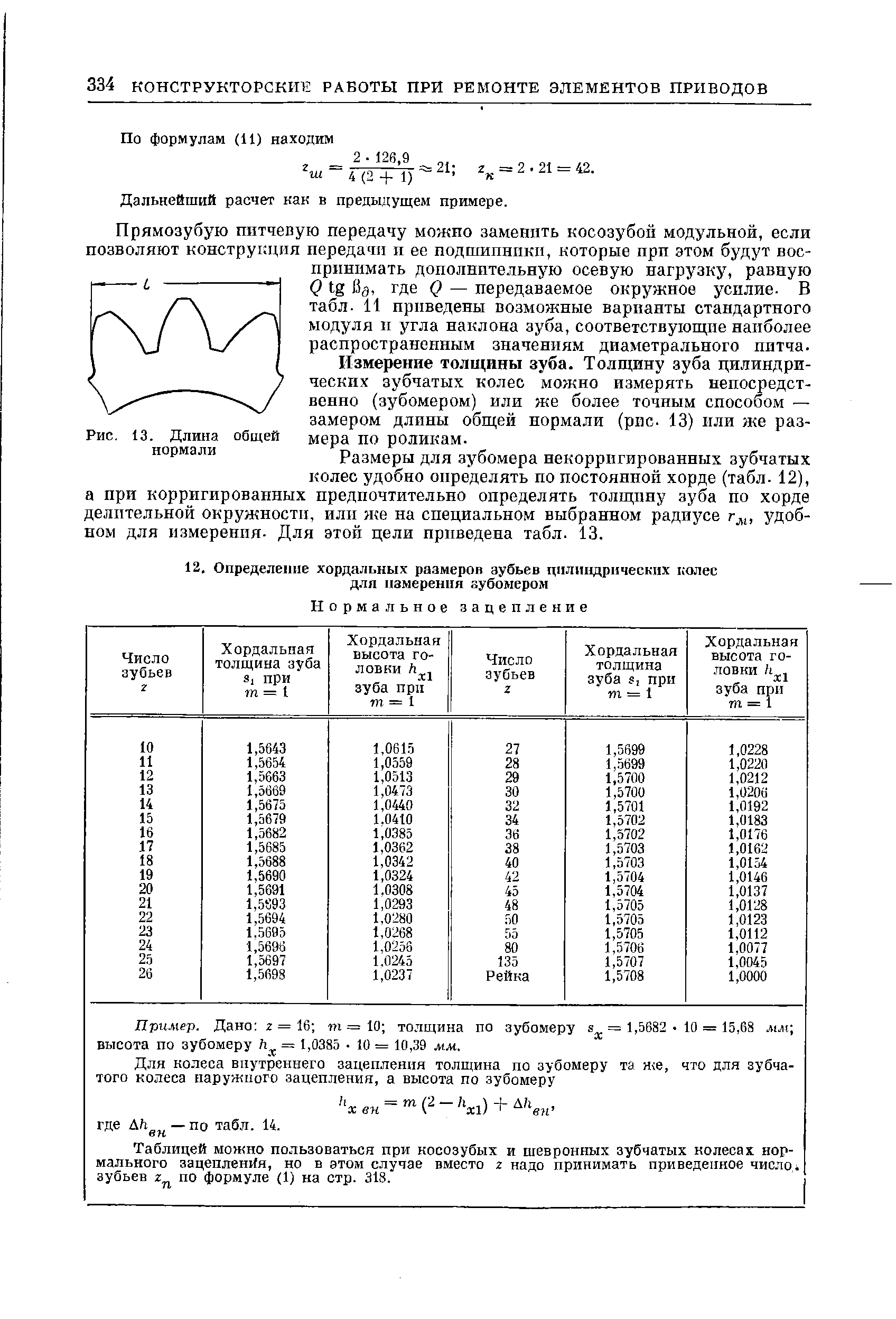
1.2. Длина общей нормали
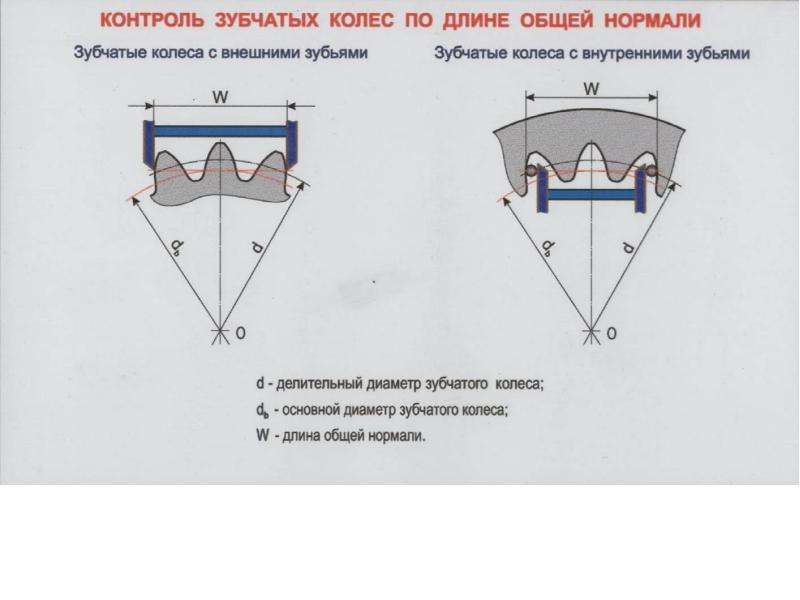
Касательную к основной окружности зубчатого колеса, которая пересекает z
w
зубьев его и является нормалью к обеим крайним эвольвентам, называют общей нормалью
.
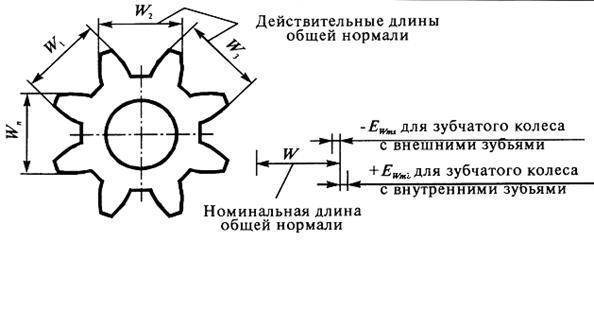
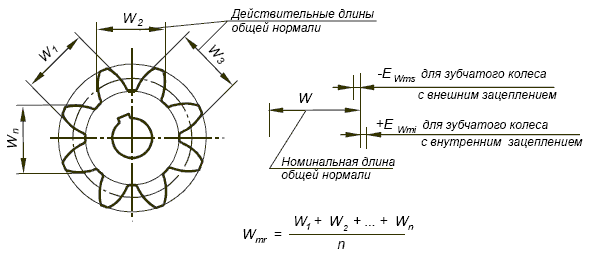
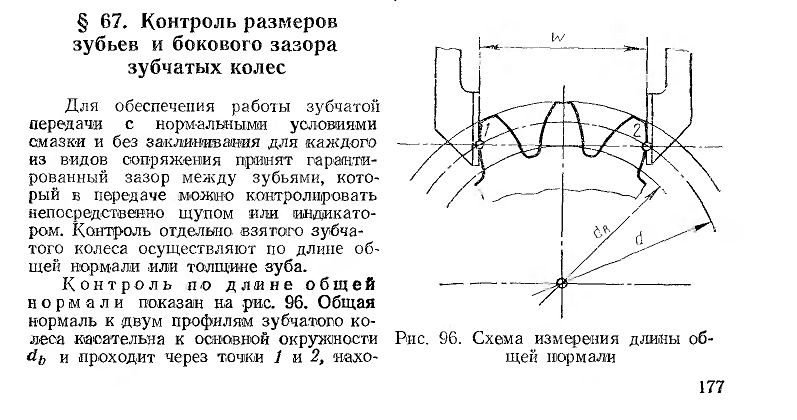
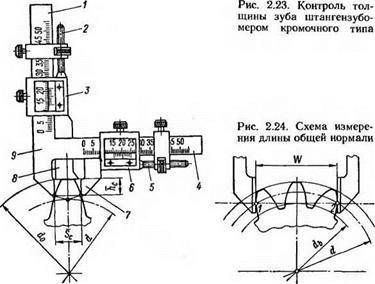
Расстояние между разноименными боковыми поверхностями зубьев цилиндрического колеса по общей нормали к этим поверхностям называют длиной общей нормали
W
(рис. 2).
Длина общей нормали не зависит от того, в каких точках профилей зубьев эта нормаль пересекает две встречные эвольвенты. Изменение длины общей нормали пропорционально изменению смещения исходного контура xm
зуборезного инструмента
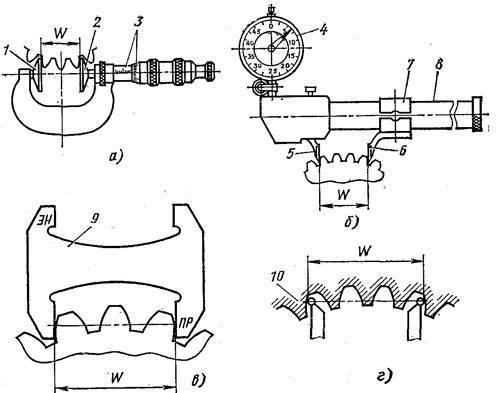
Важно также, что контроль размера w
не связан с какой-либо вспомогательной базой для установки мерительного инструмента
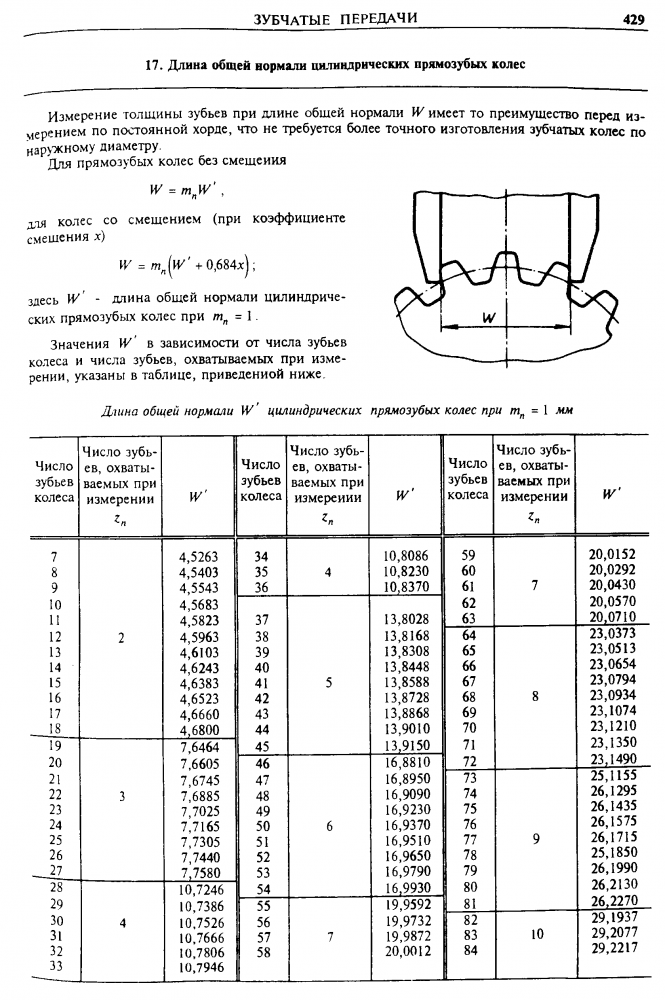
Указанные свойства общей нормали показывают преимущество данного способа контроля толщины зуба колеса. Этот размер можно измерять штангенциркулем, микрометром, специальной предельной скобой.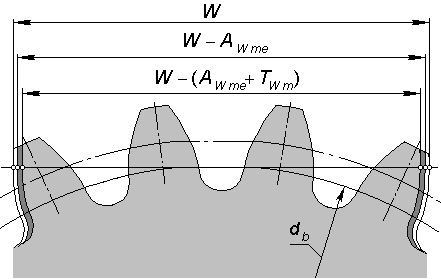
Рис. 2Длину общей нормали для цилиндрических колес с внешними прямыми зубьями
рассчитывают по следующей формуле ,где m
– модуль, мм; a – угол профиля исходного контура, по стандарту ГОСТ 13755-81 a =20 0 ; z
w
– число зубьев в длине общей нормали; x
– коэффициент смещения; z
– число зубьев контролируемого колеса; inv a – эвольвентный угол, соответствующий углу профиля a, для прямозубых колес inva =
tga –
a.
Длину общей нормали для цилиндрических колес с внешними косыми зубьями
рассчитывают по аналогичной формуле,где m
n
– нормальный модуль, мм;
, а торцовый угол профиля исходного контура . Здесь – задаваемый чертежом зубчатого колеса делительный угол наклона линии зуба.
Для косозубого колеса длину общей нормали измеряют под основным углом наклона линии зуба b
к торцу колеса, а возможность замера проверяют при достаточной ширине зубчатого венца b
по условиюb
і w
sin b
,где sin b
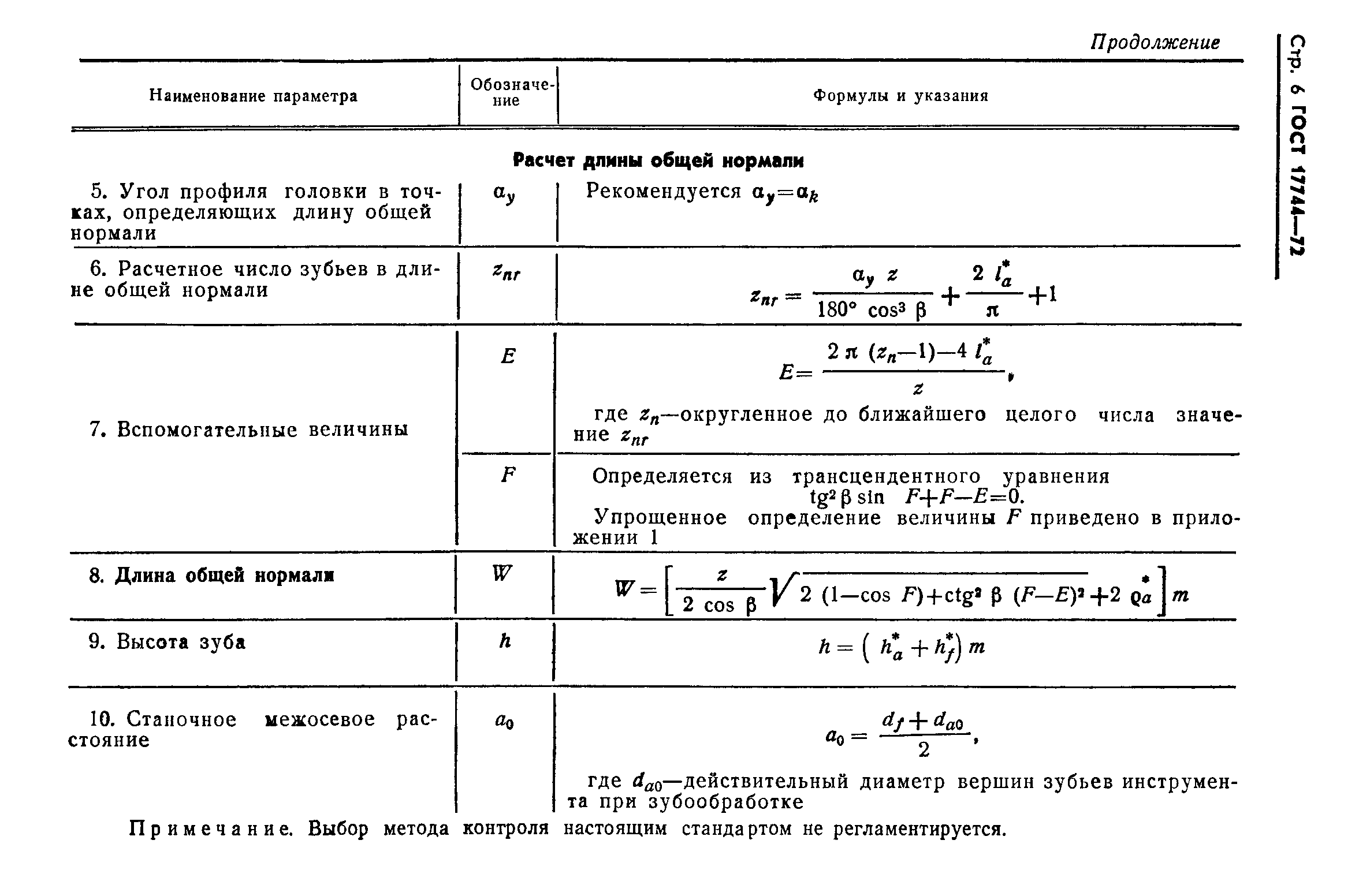
= sin·cos.Число зубьев в длине общей нормали z
w
для цилиндрических колес с прямыми зубьями должно удовлетворять условию,когда , ,Здесь a
– угол профиля в точке на окружности вершин зубьев; l
– угол профиля в граничной точке.
При небольших коэффициентах смещения (x
1) для определения z
w
можно пользоваться упрощенной формулой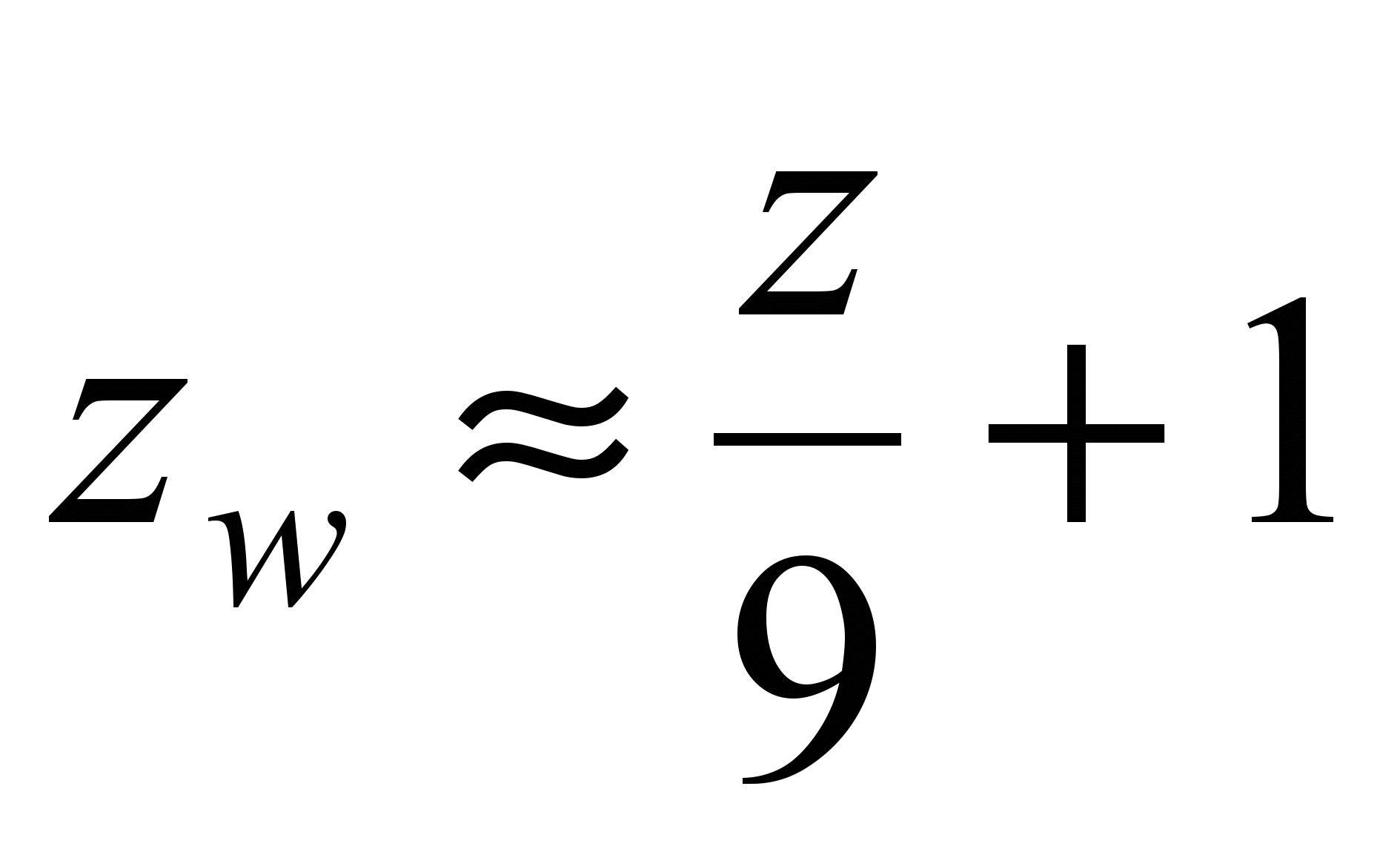
с округлением полученного значения до ближайшего целого значения.
Исходные данные и замеры
На практике перед инженерами часто встает задача определения модуля реально существующей шестерни для ее ремонта или замены. При этом случается и так, что конструкторской документации на эту деталь, как и на весь механизм, в который она входит, обнаружить не удается.
Самый простой метод — метод обкатки. Берут шестерню, для которой характеристики известны. Вставляют ее в зубья тестируемой детали и пробуют обкатать вокруг. Если пара вошла в зацепление — значит их шаг совпадает. Если нет — продолжают подбор. Для косозубой выбирают подходящую по шагу фрезу.
Такой эмпирический метод неплохо срабатывает для зубчатых колес малых размеров.
Для крупных, весящих десятки, а то и сотни килограмм, такой способ физически нереализуем.
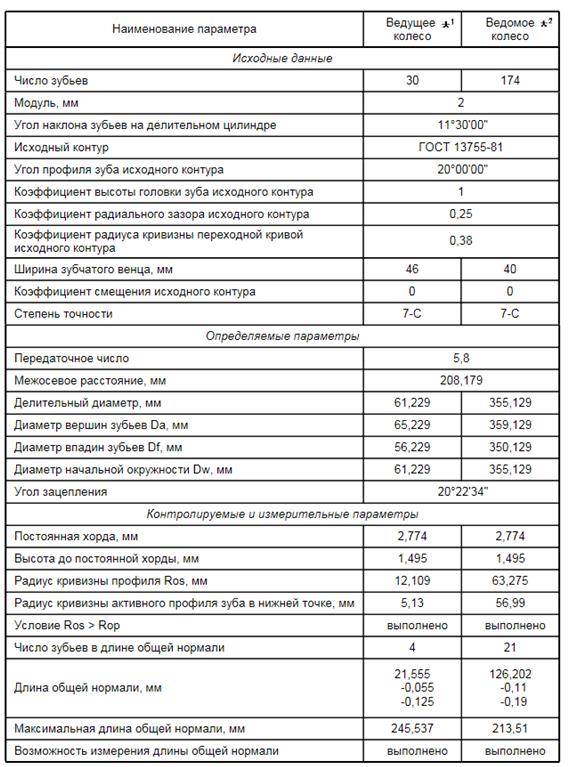
Результаты расчетов
Для более крупных потребуются измерения и вычисления.
Как известно, модуль равен диаметру окружности выступов, отнесенному к числу зубов плюс два:
m=De/(z+2)
Последовательность действий следующая:
- измерить диаметр штангенциркулем;
- сосчитать зубцы;
- разделить диаметр на z+2;
- округлить результат до ближайшего целого числа.
Зубец колеса и его параметры
Данный метод подходит как для прямозубых колес, так и для косозубых.
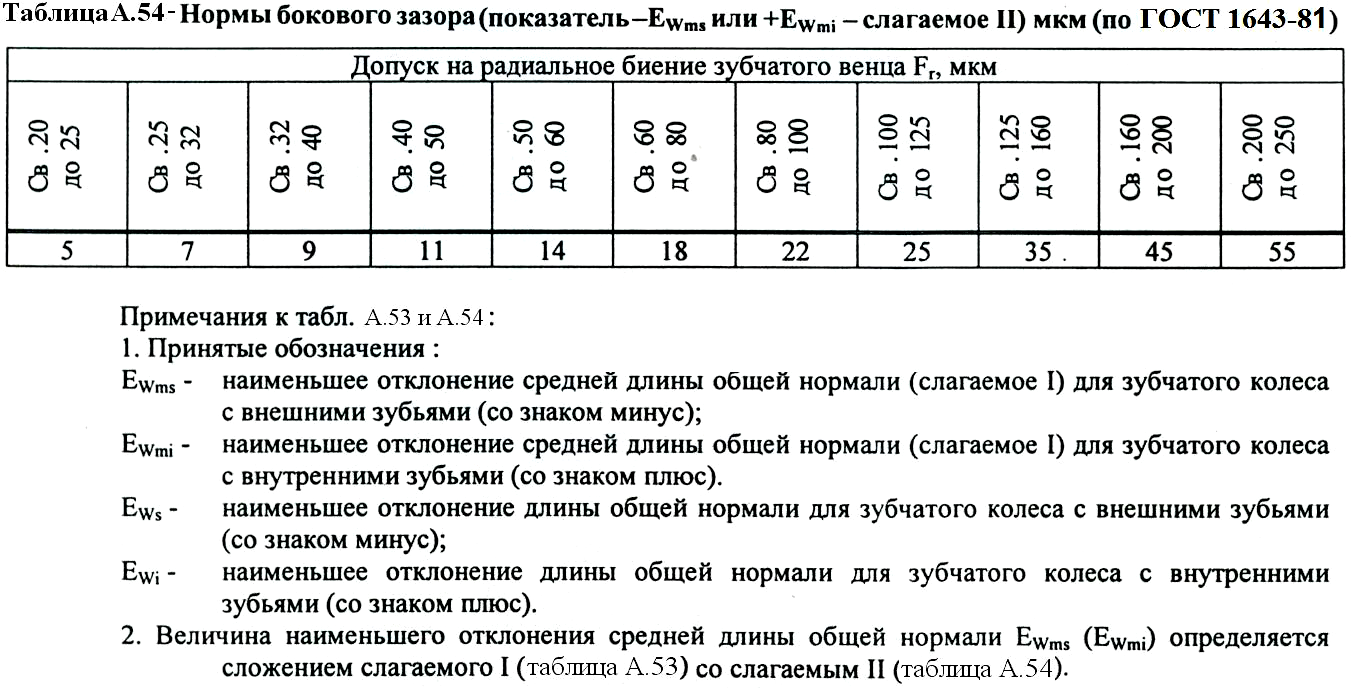
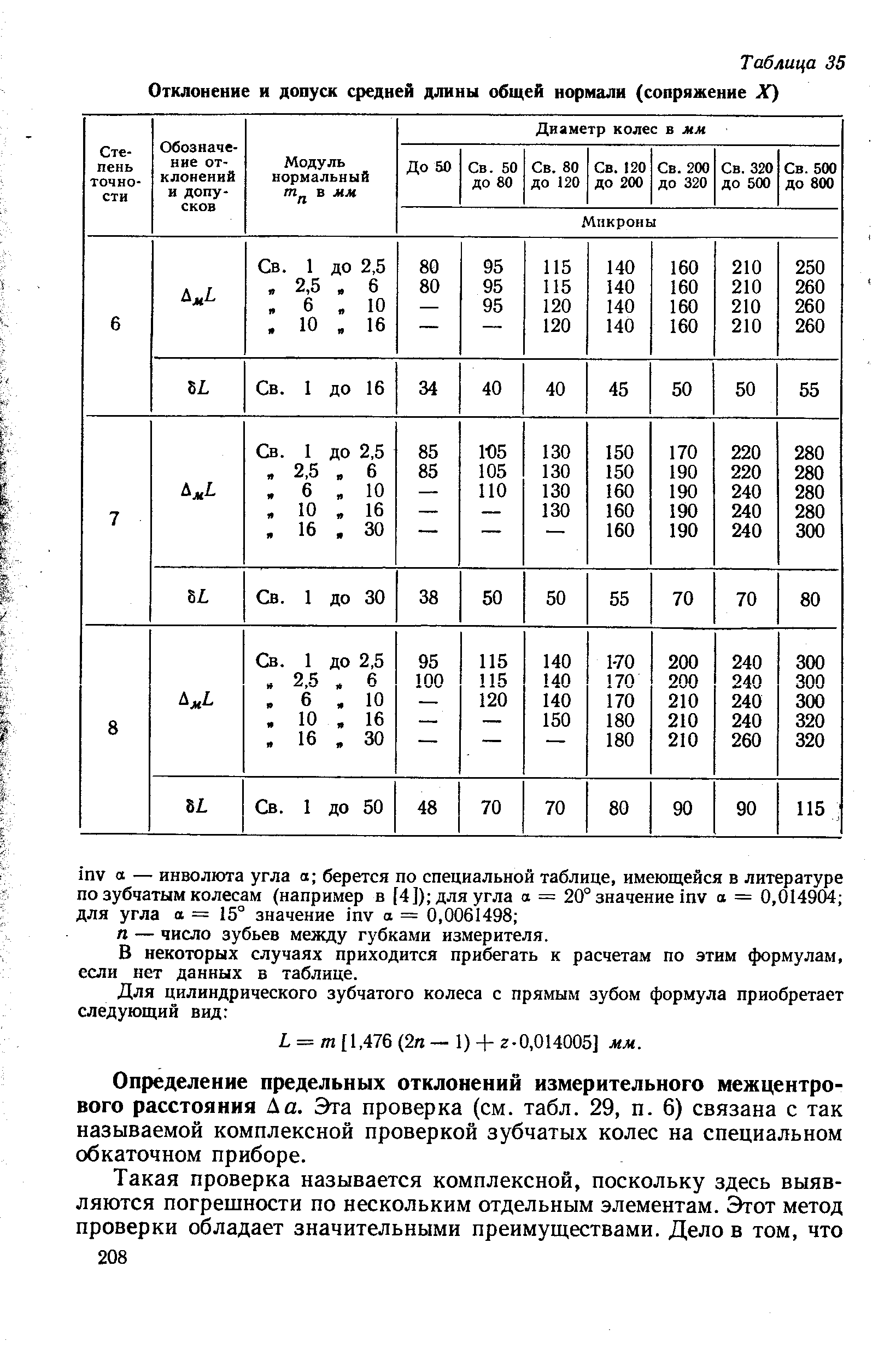
1.3. Допуски на измерительные размеры цилиндрических зубчатых колес
Рассмотренные выше формулы для вычисления номинальных измерительных размеров цилиндрических зубчатых колес гарантируют беззазорное зацепление колес в передаче. В реальных зубчатых передачах должен быть обеспечен гарантированный боковой зазор
с целью устранения заклинивания зубьев при работе под нагрузкой в результате температурных деформаций деталей передачи, а также для размещения слоя смазки на рабочих профилях зубьев. Боковой зазор в зацеплении необходим также для компенсации погрешностей изготовления и монтажа передачи. Он определяется в основном величиной межосевого расстояния a
w
передачи и толщиной s
зубьев колес.
Стандартом на эвольвентные зубчатые цилиндрические передачи (ГОСТ 1643-81) установлено восемь видов допусков на боковой зазор: h
, d
, c
, b
, a
, z
, y
, x
(обозначения допусков расположены в порядке возрастания величины допуска). Принятая величина гарантированного бокового зазора является основой для назначения вида сопряжения
зубчатых колес. Этим же стандартом предусмотрено шесть видов сопряжения: H
– нулевой зазор, E
– малый зазор, C
и D
– уменьшенный зазор, B
– нормальный зазор, A
– увеличенный зазор. Сопряжения видов Н
, Е
и С
требуют повышенной точности изготовления зубьев колес. Их применяют для реверсируемых передач при высоких требованиях к кинематической точности передачи, а также при наличии крутильных колебаний валов передачи. Чаще всего в среднем машиностроении используют передачи с видами сопряжения В
и С
. При отсутствии специальных требований к зубчатой передаче с каждым видом сопряжения употребляется определенный вид допуска на боковой зазор, обозначаемый строчной буквой, аналогичной букве вида сопряжения (например, А
– а
, В
– в
, С
– с
и т. д.).
Поле допуска на измерительный размер зубчатого колеса всегда направлено в тело зуба, поэтому предельные отклонения измерительного размера (верхнее и нижнее) всегда имеют отрицательные значения .
Основные ошибки самостоятельной замены
Несмотря на предельно простую технологию, автолюбители часто допускают при замене венца следующие ошибки:
- перед тем, как снять зубчатый обод, следует произвести ревизию боковой плоскости маховика под сцепление, и отверстий для крепежных болтов;
- установка с перегревом отдельных участков венца приведет к быстрому износу зубьев именно на этих местах, так как происходит отпуск стали;
- наружный диаметр зубьев должен иметь фаску для плавного зацепления с бендиксом стартера без ударов.
Для того, чтобы уменьшить износ двигателя и увеличить приемистость машины на высоких оборотах, маховик часто облегчают. Из-за наличия дополнительных отверстий на наружном диаметре диска в зоне, примыкающей к зубчатому ободу, венец часто приваривается к диску.
Таким образом, венец можно заменить собственными силами при значительной выработке профиля зуба на отдельных участках. Снять обод можно на холодную, а при установке потребуется нагрев до 200 градусов максимум.
