Кубическая гранецентрированная решетка

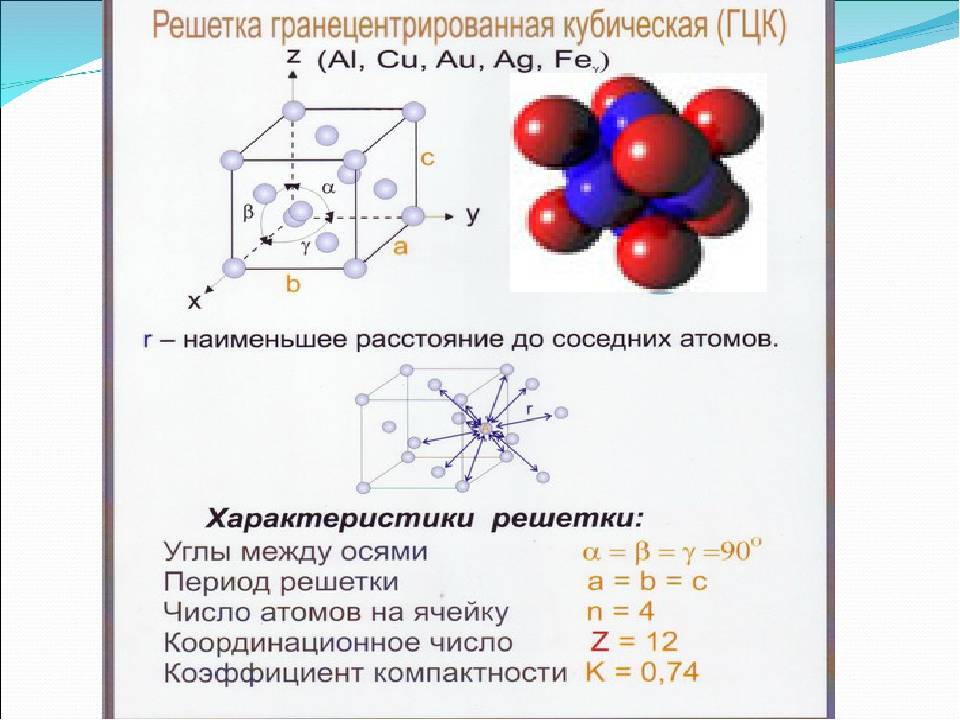
Общее понятие о металлах

«Химия. 9 класс» — это учебник, по которому проходят обучение школьники. Именно в нем подробно изучаются металлы. Рассмотрению их физических и химических свойств отведена большая глава, ведь разнообразие их чрезвычайно велико.

Именно с этого возраста рекомендуют давать детям представление о данных атомах и их свойствах, ведь подростки уже вполне могут оценить значение подобных знаний. Они прекрасно видят, что окружающее их разнообразие предметов, машин и прочих вещей имеет в своей основе как раз металлическую природу.

Что же такое металл? С точки зрения химии, к данным атомам принято относить те, что имеют:

• малое число электронов на внешнем уровне;
• проявляют сильные восстановительные свойства;
• имеют большой атомный радиус;
• как простые вещества обладают рядом специфических физических свойств.

Основу знаний об этих веществах можно получить, если рассмотреть атомно-кристаллическое строение металлов. Именно оно объясняет все особенности и свойства данных соединений.

В периодической системе для металлов отводится большая часть всей таблицы, ведь они образуют все побочные подгруппы и главные с первой по третью группу. Поэтому их численное превосходство очевидно. Самыми распространенными являются:

• кальций;
• натрий;
• титан;
• железо;
• магний;
• алюминий;
• калий.

Все металлы имеют ряд свойств, которые позволяют объединять их в одну большую группу веществ. В свою очередь, эти свойства объясняет именно кристаллическое строение металлов.

Смотреть галерею

Произвольный набор атомов

Тень обратной решетки интенсивности граненого углеродного пентакона, состоящего из 118 атомов, загорается красным при дифракции при пересечении сферы Эвальда.

Один путь к обратной решетке произвольного набора атомов происходит от идеи рассеянных волн в пределах Фраунгофера (дальнего расстояния или задней фокальной плоскости линзы) как суммы амплитуд в стиле Гюйгенса от всех точек рассеяния (в этот случай от каждого отдельного атома). Эта сумма обозначается комплексной амплитудой F в приведенном ниже уравнении, потому что это также преобразование Фурье (как функция пространственной частоты или обратного расстояния) эффективного потенциала рассеяния в прямом пространстве:

Fг→знак равно∑jзнак равно1Nжjг→е2πяг→⋅р→j.{\ Displaystyle F = \ sum _ {j = 1} ^ {N} f_ {j} \ left e ^ {2 \ pi i {\ vec {g}} \ cdot {\ vec {r}} _ {j}}.}

Здесь g = q / (2π) – вектор рассеяния q в единицах кристаллографа, N – число атомов, f j – атомный коэффициент рассеяния для атома j и вектор рассеяния g , а r j – положение вектора атом j

Обратите внимание, что фаза Фурье зависит от выбора начала координат.. Для частного случая бесконечного периодического кристалла амплитуда рассеяния F = MF hkl от M элементарных ячеек (как и в случаях выше) оказывается ненулевой только для целых значений , где (часkл){\ displaystyle (hkl)}

Для частного случая бесконечного периодического кристалла амплитуда рассеяния F = MF hkl от M элементарных ячеек (как и в случаях выше) оказывается ненулевой только для целых значений , где (часkл){\ displaystyle (hkl)}

Для частного случая бесконечного периодического кристалла амплитуда рассеяния F = MF _hkl от M элементарных ячеек (как и в случаях выше) оказывается ненулевой только для целых значений , где (часkл){\ displaystyle (hkl)}

Fчасkлзнак равно∑jзнак равно1мжjгчасkле2πя(частыj+kvj+лшj){\ displaystyle F_ {hkl} = \ sum _ {j = 1} ^ {m} f_ {j} \ left e ^ {2 \ pi i \ left (hu_ {j} + kv_ {j} + lw_ {j} \ right)}}

когда j = 1, m атомов внутри элементарной ячейки, дробные индексы решетки которых равны соответственно {u _j , v _j , w _j }. Конечно, чтобы учесть эффекты, связанные с конечным размером кристалла, вместо этого следует использовать свертку формы для каждой точки или приведенное выше уравнение для конечной решетки.

Независимо от того, является ли массив атомов конечным или бесконечным, можно также представить себе “обратную решетку интенсивности” I [ g ], которая связана с решеткой амплитуд F через обычное соотношение I = F * F, где F * – комплексное сопряжение F Поскольку преобразование Фурье обратимо, конечно, этот акт преобразования в интенсивность отбрасывает «всю информацию, кроме 2-го момента» (то есть фазы). Таким образом, для случая произвольного набора атомов обратная решетка интенсивности имеет вид:

яг→знак равно∑jзнак равно1N∑kзнак равно1Nжjг→жkг→е2πяг→⋅р→jk.{\ displaystyle I = \ sum _ {j = 1} ^ {N} \ sum _ {k = 1} ^ {N} f_ {j} \ left f_ {k} \ left e ^ {2 \ pi i {\ vec {g}} \ cdot {\ vec {r}} _ {jk}} .}

Здесь r _jk – векторное расстояние между атомом j и атомом k. Это также можно использовать для прогнозирования влияния формы нанокристаллита и тонких изменений ориентации луча на обнаруженные дифракционные пики, даже если в некоторых направлениях толщина кластера составляет всего один атом. С другой стороны, расчеты рассеяния с использованием обратной решетки в основном учитывают падающую плоскую волну. Таким образом, после первого взгляда на эффекты обратной решетки (кинематического рассеяния), уширение луча и эффекты многократного рассеяния (т.е. динамические ) также могут быть важны для рассмотрения.

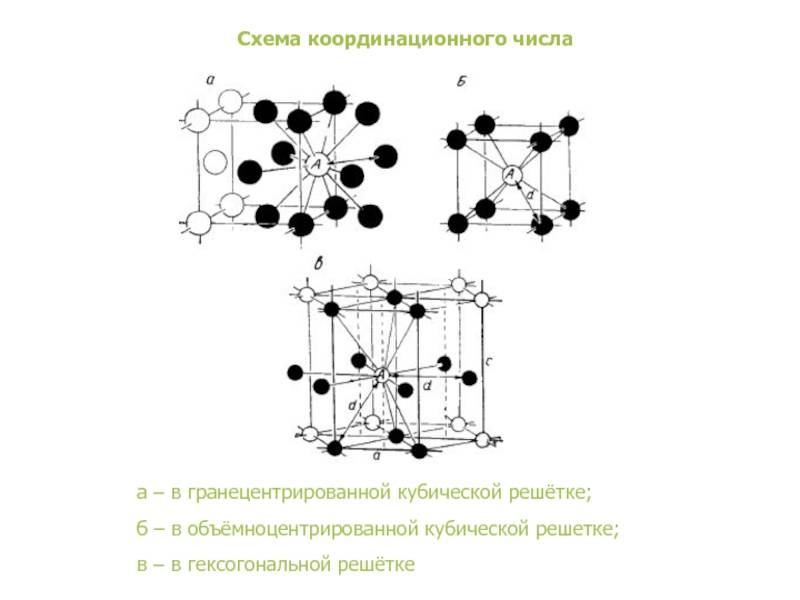
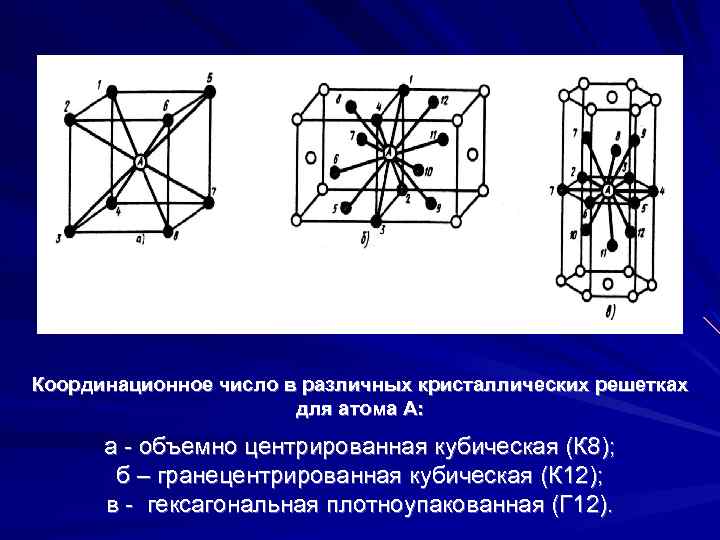
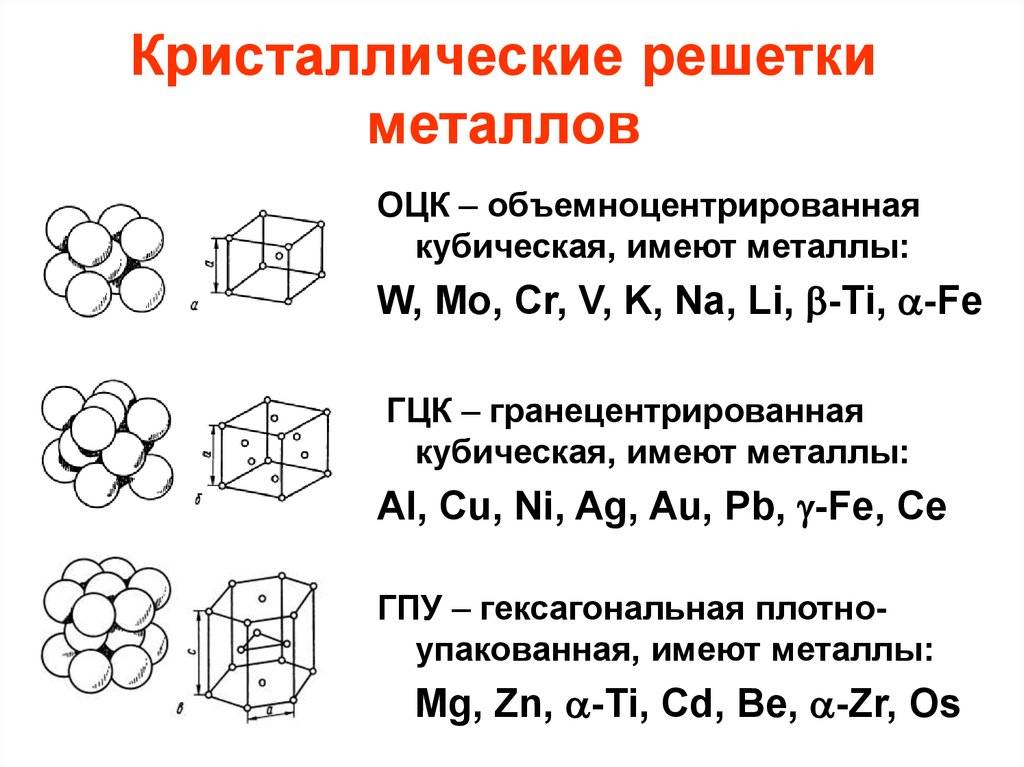
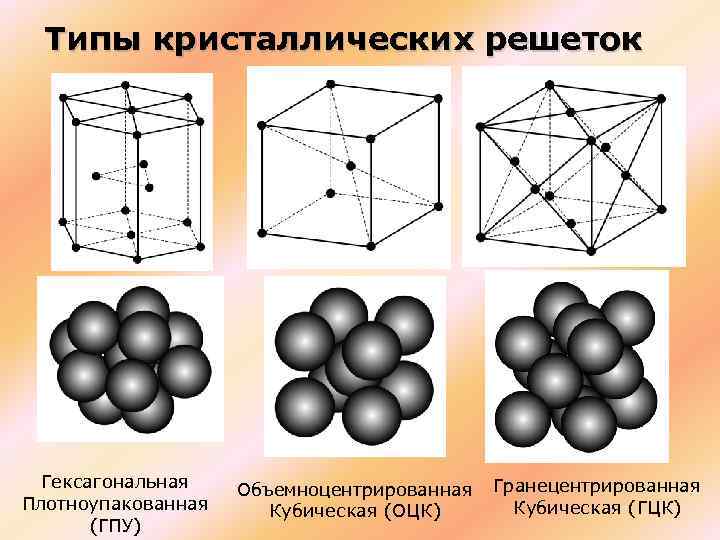
А) объемноцентрированная кубическая

б) гранецентрированная кубическая

в) гексагональная плотноупакованная

Некоторые металлы, в зависимости от температуры, могут иметь различный тип кристаллической решётки, т.е. могут существовать в различных кристаллических модификаций.

Полиморфизм (аллотропия) – когда металл имеет разную кристаллическую решётку в зависимости от условия образования. Переход одной решётки в другую называется полиморфное или аллотропическое состояние. Полиморфные превращения в металлах происходят при изменении температуры. Так, при температуре свыше 723°С железо переходит из α – модификации в γ – модификацию, при этом изменяются физико-механические свойства металла.

Чтобы отличить одну кристаллическую решётку железа Fe от другой ставят значок α или γ

В монокристаллах свойства металла по различным направлениям различны – это явление носит название анизотропией.

В реальных поликристаллических металлах свойства по любому направлению одинаково – это явление называется изотропией.

Металлы обладают целым рядом общих свойств:

Высокая электо- и теплопроводимость

Характерный металлический блеск

Положительный коэффициент электросопротивления

Способность к значительной пластической деформации

Одним из самых распространенных материалов, с которым всегда предпочитали работать люди, был металл. В каждую эпоху предпочтение отдавалось разным видам этих удивительных веществ. Так, IV-III тысячелетия до нашей эры считаются веком хальколита, или медным. Позже его сменяет бронзовый, а затем в силу вступает тот, что и по сей день является актуальным — железный.

Сегодня вообще сложно представить, что когда-то можно было обходиться без металлических изделий, ведь практически все, начиная от предметов быта, медицинских инструментов и заканчивая тяжелой и легкой техникой, состоит из этого материала или включает в свой состав отдельные части из него. Почему же металлы сумели завоевать такую популярность? В чем проявляются особенности и как это заложено в их строении, попробуем разобраться далее.

Пустоты в элементарной ячейке

Визуализация кубической элементарной ячейки алмаза: 1. Компоненты элементарной ячейки, 2. Одна элементарная ячейка, 3. Решетка из 3 x 3 x 3 элементарных ячеек.

Пустоты в элементарной ячейке также известны как промежуточные участки или отверстия. Это пустое пространство, которое существует между упаковками атомов (сфер) в элементарных ячейках.

Отверстия легко увидеть, если вы попытаетесь сложить круги вместе. Независимо от того, насколько близко вы их подберете или как вы их разместите, у вас будет пустое пространство между ними. То же самое верно и в элементарной ячейке, независимо от того, как атомы расположены, между атомами будут присутствовать промежуточные узлы. Эти узлы или дыры могут быть заполнены другими атомами. Изображение с упакованными кружками – это только 2D-представление. В кристаллической решетке атомы (сферы) будут упакованы в трехмерном виде. Это приводит к появлению межузельных узлов различной формы в зависимости от расположения атомов в решетке.

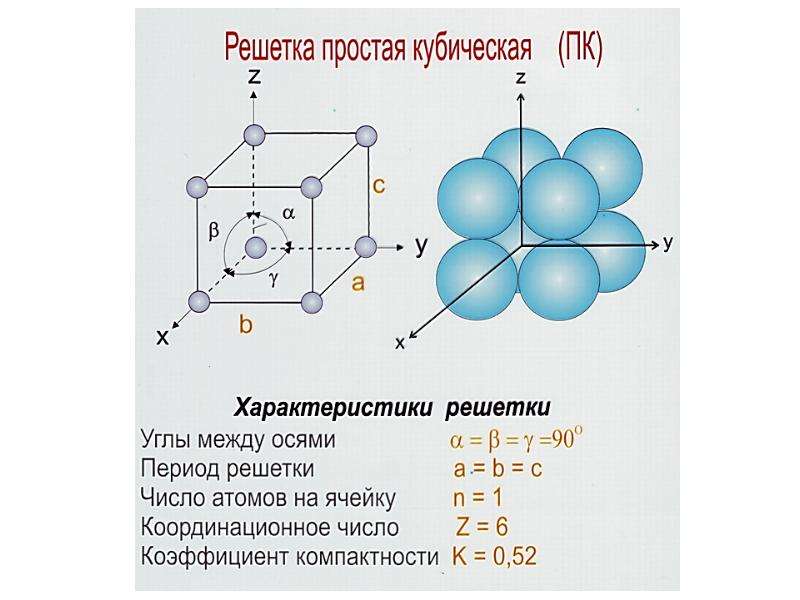
Простая кубическая элементарная ячейка со стопками атомов, расположенными так, как если бы в восьми углах куба, образовала бы одно кубическое отверстие или пустоту в центре.

Плотноупакованная элементарная ячейка, как гранецентрированная кубическая, так и гексагональная плотноупакованная, может образовывать два отверстия разной формы. Глядя на три зеленые сферы на иллюстрации шестиугольной упаковки, они образуют отверстие в форме треугольника. Если атом расположен на вершине этого треугольного отверстия, он образует тетраэдрическое межузельное отверстие. Если три атома в верхнем слое повернуты и их треугольное отверстие находится поверх этого, это образует октаэдрическое межузельное отверстие. В плотноупакованной структуре имеется 4 атома на элементарную ячейку, и она будет иметь 4 октаэдрических пустоты (соотношение 1: 1) и 8 тетраэдрических пустот (соотношение 1: 2) на элементарную ячейку. Тетраэдрическая пустота меньше по размеру и может вместить атом с радиусом в 0,225 раза больше размера атомов, составляющих решетку. В октаэдрическую пустоту может поместиться атом с радиусом в 0,441 раза превышающим размер атомов, составляющих решетку. Атом, заполняющий это пустое пространство, может быть больше, чем это идеальное отношение радиусов, что приведет к искажению решетки из-за выталкивания окружающих атомов, но оно не может быть меньше этого отношения.

Объемно-центрированная кубическая элементарная ячейка имеет шесть октаэдрических пустот, расположенных в центре каждой грани элементарной ячейки, и двенадцать дополнительных, расположенных в середине каждого края той же ячейки, в общей сложности шесть октаэдрических пустот. Вдобавок есть 24 тетраэдрических пустоты, расположенных на квадратном расстоянии вокруг каждой октаэдрической пустоты, всего двенадцать чистых тетраэдрических пустот. Эти тетраэдрические пустоты не являются локальными максимумами и технически не являются пустотами, но иногда они появляются в многоатомных элементарных ячейках.

Одной из важных характеристик кристаллической структуры является фактор упаковки атомов . Это рассчитывается исходя из предположения, что все атомы являются идентичными сферами, с достаточно большим радиусом, чтобы каждая сфера упиралась в следующую. Фактор упаковки атомов – это доля пространства, заполненного этими сферами.

Предполагая , один атом за решетку точки, в примитивной кубической решетке с длиной стороны кубы а , радиус шара будет 2 и атомный фактор упаковки оказывается около 0,524 (что является довольно низким). Это означает, что объем элементарной ячейки, фактически занятый атомами, составляет всего 52,4%. Точно так же в ОЦК решетке фактор упаковки атомов составляет 0,680, а в ГЦК – 0,740. Значение ГЦК является наивысшим теоретически возможным значением для любой решетки, хотя есть и другие решетки, которые также достигают того же значения, например, гексагональная плотноупакованная ( ГПУ ) и одна версия тетраэдрической ОЦК .

Как правило, поскольку атомы в твердом теле притягиваются друг к другу, более плотно упакованные атомы имеют тенденцию быть более распространенными. (Хотя могут иметь место неплотно упакованные структуры, например, если орбитальная гибридизация требует определенных валентных углов .) Соответственно, примитивная кубическая структура с особенно низким коэффициентом упаковки атомов встречается редко в природе, но встречается в полонии . ОЦК и ГЦК , с их более высокой плотностью, оба весьма распространены в природе. Примеры ОЦК включают железо , хром , вольфрам и ниобий . ПримерыГЦК включают алюминий , медь , золото и серебро .

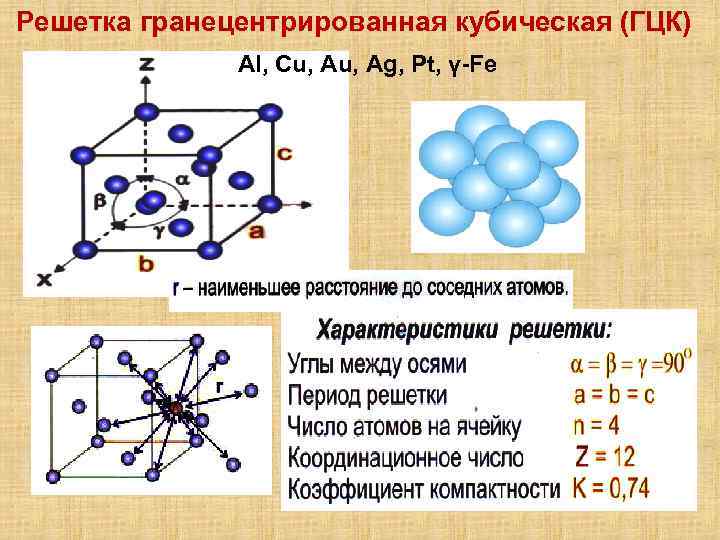
Кристаллическая решетка металлов

Все металлы, затвердевающие в нормальных условиях, представляют собой кристаллические вещества, то есть укладка атомов в них характеризуется определенным порядком – периодичностью, как по различным направлениям, так и по различным плоскостям. Этот порядок определяется понятием кристаллическая решетка. Другими словами, кристаллическая решетка это воображаемая пространственная решетка, в узлах которой располагаются частицы, образующие твердое тело.

Элементарная ячейка – элемент объема из минимального числа атомов, многократным переносом которого в пространстве можно построить весь кристалл. Элементарная ячейка характеризует особенности строения кристалла. Основными параметрами кристалла являются:

• размеры ребер элементарной ячейки. a, b, c – периоды решетки – расстояния между центрами ближайших атомов (в одном направлении выдерживаются строго определенными);
• углы между осями (α, β, χ);
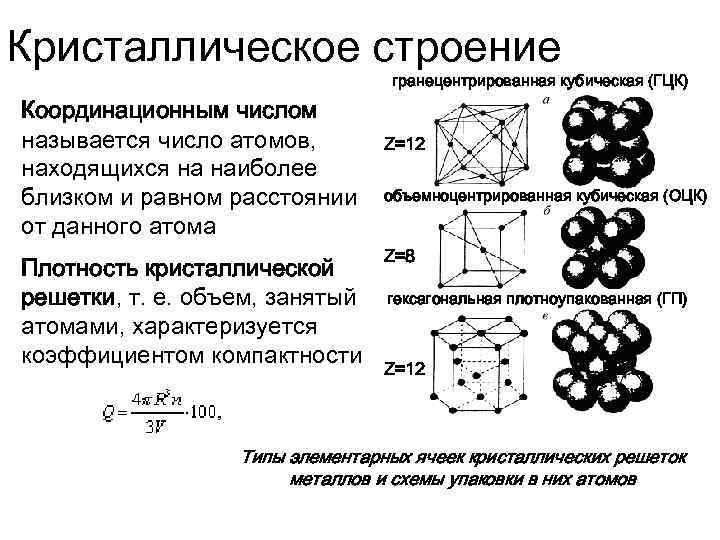
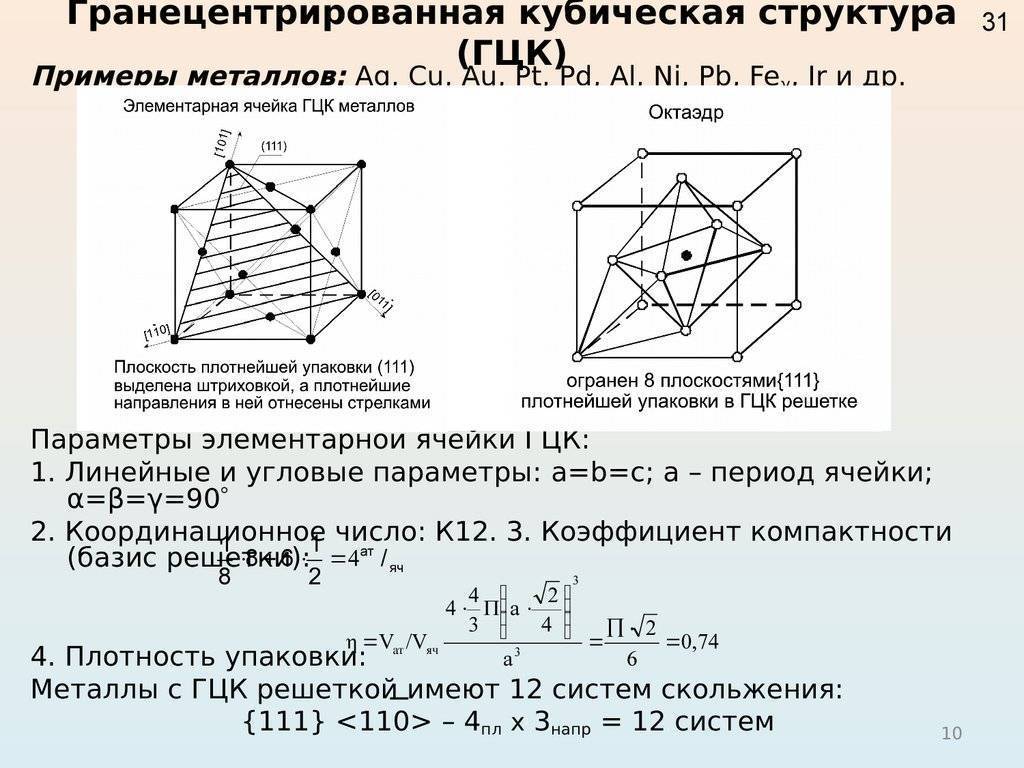
• координационное число (К) указывает на число атомов, расположенных на ближайшем одинаковом расстоянии от любого атома в решетке;
• базис решетки количество атомов, приходящихся на одну элементарную ячейку решетки;
• плотность упаковки атомов в кристаллической решетке – объем, занятый атомами, которые условно рассматриваются как жесткие шары. Ее определяют как отношение объема, занятого атомами к объему ячейки (для объемно-центрированной кубической решетки – 0,68, для гранецентрированной кубической решетки – 0,74).

Схема кристаллической решетки

Классификация возможных видов кристаллических решеток была проведена французским ученым О. Браве, соответственно они получили название «решетки Браве». Всего для кристаллических тел существует четырнадцать видов решеток, разбитых на четыре типа:

• примитивный – узлы решетки совпадают с вершинами элементарных ячеек;
• базоцентрированный – атомы занимают вершины ячеек и два места в противоположных гранях;
• объемно-центрированный – атомы занимают вершины ячеек и ее центр;
• гранецентрированный – атомы занимают вершины ячейки и центры всех шести граней.

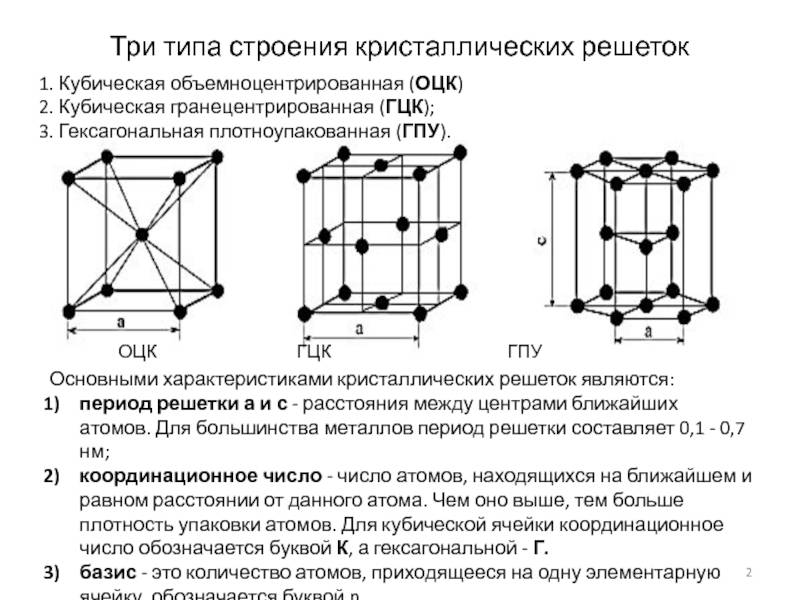
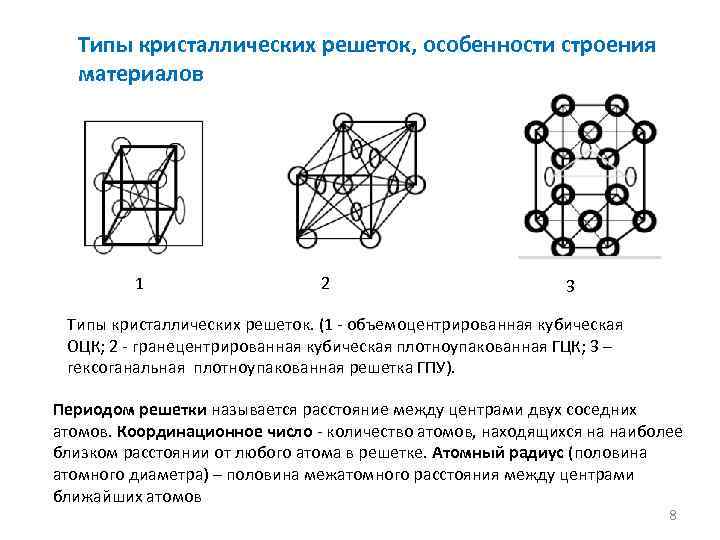
Типы кристаллических решеток

Рис. 2: а – объемно-центрированная кубическая; б– гранецентрированная кубическая; в – гексагональная плотноупакованная

Основными типами кристаллических решеток являются:

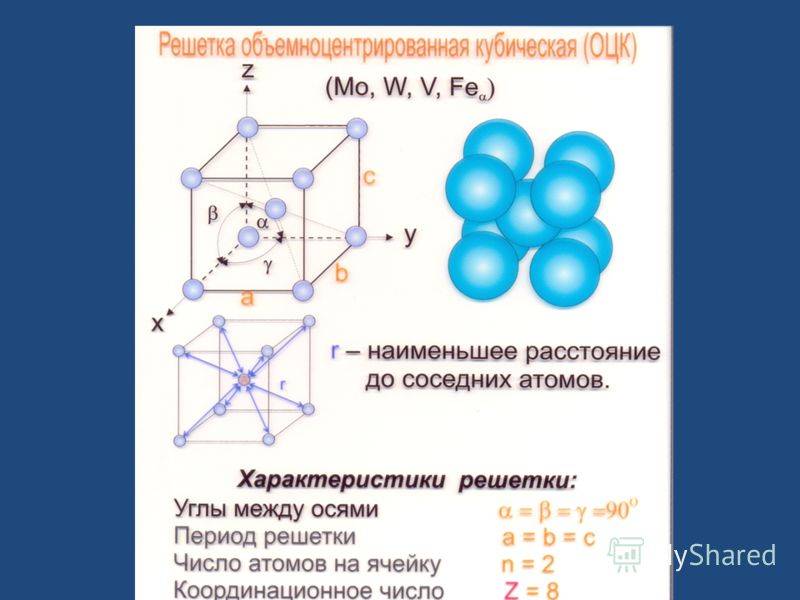
1. Объемно — центрированная кубическая (ОЦК) (рисунок 2, позиция а), атомы располагаются в вершинах куба и в его центре (V, W, Ti, Fe_α)
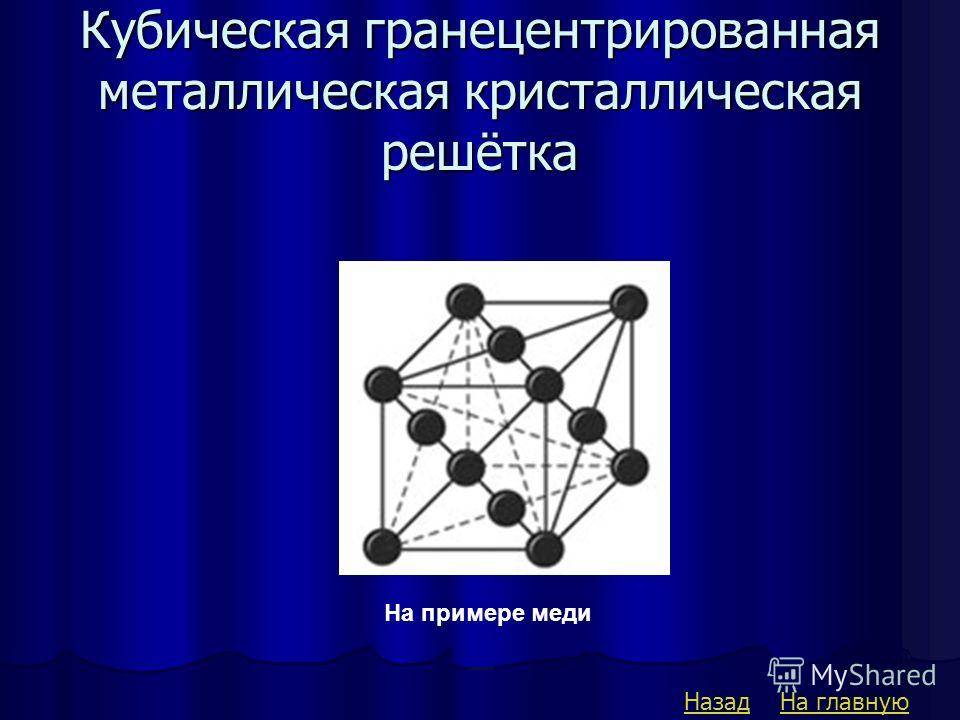
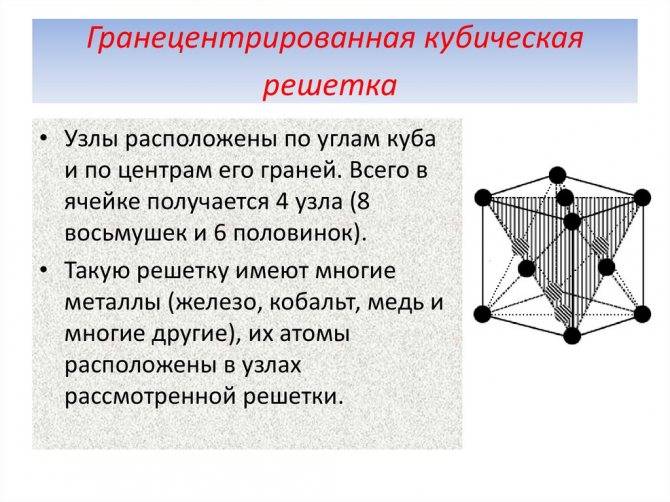
2. Гранецентрированная кубическая (ГЦК) (рисунок 2, позиция б), атомы рассполагаются в вершинах куба и по центру куждой из 6 граней (Ag, Au, Fe_γ)
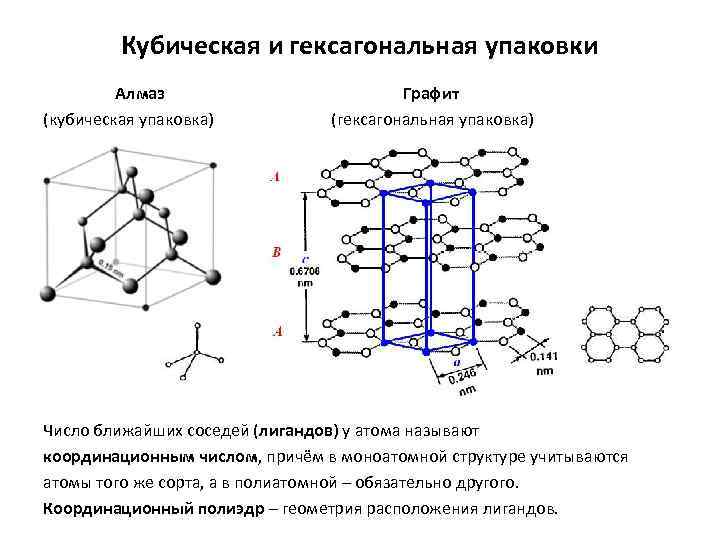
3. Гексагональная, в основании которой лежит шестиугольник:
   • — простая – атомы располагаются в вершинах ячейки и по центру 2 оснований (углерод в виде графита);

• — плотноупакованная (ГПУ) – имеется 3 дополнительных атома в средней плоскости (цинк).

Полиморфизм

Кварц – одна из нескольких кристаллических форм кремнезема SiO ₂ . Наиболее важные формы кремнезема включают: α-кварц , β-кварц , тридимит , кристобалит , коэсит и стишовит .

Полиморфизм – это появление нескольких кристаллических форм материала. Он содержится во многих кристаллических материалах, включая полимеры , минералы и металлы . Согласно правилам фазового равновесия Гиббса, эти уникальные кристаллические фазы зависят от интенсивных переменных, таких как давление и температура. Полиморфизм связан с аллотропией , которая относится к элементарным твердым телам . Полная морфология материала описывается полиморфизмом и другими переменными, такими как габитус кристаллов , аморфная фракция или кристаллографические дефекты . Полиморфы обладают разной стабильностью и могут спонтанно и необратимо превращаться из метастабильной формы (или термодинамически нестабильной формы) в стабильную форму при определенной температуре. Они также имеют разные температуры плавления , растворимость и дифрактограммы рентгеновских лучей .

Хорошим примером этого является кварцевая форма диоксида кремния или SiO ₂ . В подавляющем большинстве силикатов атом Si имеет тетраэдрическую координацию по 4 атомам кислорода. Все кристаллические формы, кроме одной, включают тетраэдрические звенья {SiO ₄ }, связанные вместе общими вершинами в разном расположении. В разных минералах тетраэдры демонстрируют разную степень сетки и полимеризации. Например, они встречаются поодиночке, соединены вместе попарно, в более крупные конечные кластеры, включая кольца, цепочки, двойные цепи, листы и трехмерные каркасы. Минералы классифицируются на группы на основе этих структур. В каждой из 7 термодинамически стабильных кристаллических форм или полиморфов кристаллического кварца только 2 из 4 ребер тетраэдров {SiO ₄ } являются общими с другими, что дает чистую химическую формулу кремнезема: SiO ₂ .

Другой пример – элементарное олово (Sn), которое является пластичным при температурах окружающей среды, но хрупким при охлаждении. Это изменение механических свойств связано с существованием двух его основных аллотропов , α- и β-олова. Два аллотропа , встречающиеся при нормальном давлении и температуре, α-олово и β-олово, более известны как серое олово и белое олово соответственно. Еще два аллотропа, γ и σ, существуют при температурах выше 161 ° C и давлениях выше нескольких ГПа. Белое олово является металлическим и представляет собой стабильную кристаллическую форму при комнатной температуре или выше. При температуре ниже 13,2 ° C олово существует в серой форме, имеющей кубическую кристаллическую структуру алмаза , подобную алмазу , кремнию или германию . Серое олово вообще не имеет металлических свойств, представляет собой тускло-серый порошкообразный материал и имеет несколько применений, кроме нескольких специализированных полупроводниковых применений. Хотя температура α – β превращения олова номинально составляет 13,2 ° C, примеси (например, Al, Zn и т. Д.) Понижают температуру перехода значительно ниже 0 ° C, и при добавлении Sb или Bi превращение может вообще не происходить.

Кристаллическая решетка и откуда она берется

Кристаллическая решетка – это вариант взаимного упорядочивания частичек в конструкции тела. Никакой кристаллической решетки не существует, зато существует взаимное расположение атомов, которое уже увидели в микроскопе, а для удобства такое расположение можно зарисовать в виде объемной схемки из шариков и их связей на прямых.

Такая объемная схемка и будет являться кристаллической решеткой.

Вид, форма и тип решетки определяются свойствами атомов, входящих в состав тела. Мы помним, что все объекты в нашей природе постоянно взаимодействует. Орбита Луны такова потому, что помимо притяжения Земли, она испытывает влияние и от других небесных тел. Мы сейчас читаем эту статью и не понимаем, что постоянно протягиваем планетой и сами притягиваем нашу планету. Такая же история и с частицами.

Взяли мы например атомы железа, расположили в пространстве. Они начали взаимодействовать друг с другом. Силы взаимного влияния заставили их расположиться в определённой последовательности. Кто-то отталкивается, кто-то притягивается, а когда их много – образуется целая система. Вот и выстраиваются частички в определенной последовательности. Такую последовательность рисуют как кристаллическую решетку.

Это очень похоже на игрушку неокуб, которая одно время продавалась буквально везде. Кубик, который был составлен из магнитных шариков прекрасно демонстрировал ячейку решетки. Добавьте к этому мысленно ещё и взаимное отталкивание и получится изучаемая нами штука.

Наверняка появился и ещё один вопрос. Ведь решетка эта по идее должна протягиваться вдоль всего кристаллического тела. В общем-то, так оно и есть в монокристаллах. Но есть ещё и поликристаллы, которые состоят из соединенных фрагментов одинаковых решеток. Тут можно подумать, что именно их мы и рисуем как кубики. Но нет, как кубики мы рисуем тот элементарный объем, который может потом выступать как строительный кирпичик для формирования большой решетки. Из таких элементарных блоков строится вся решетка как стена из кирпича. Эти блоки имеют свои названия. Вот мы и подошли к ГЦК, ОЦК и ГПУ.

Многоэлементные соединения

Соединения, которые состоят из более чем один элемент (например, бинарные соединения ) часто имеет кристаллическую структуру, основанную на кубической кристаллической системе. Здесь перечислены некоторые из наиболее распространенных.

Структура хлорида цезия

элементарная ячейка хлорида цезия

Пространственная группа структуры хлорида цезия (CsCl) называется Pm3m (в нотации Германа – Могена ) или «221» (в Международных таблицах для кристаллографии). Обозначение Strukturbericht – «B2».

Помимо самого хлорида цезия, структура также проявляется в некоторых других галогенидах щелочных металлов, когда они получены при низких температурах или высоких давлениях. Как правило, эта структура с большей вероятностью будет образована из двух элементов, ионы которых имеют примерно одинаковый размер (например, ионный радиус Cs = 167 мкм, а Cl = 181 мкм).

Координационное число каждого атома в структуре равно 8: центральный катион координируется с 8 анионами в углах куба, как показано, и аналогично центральный анион координируется с 8 катионов по углам куба.

Другими соединениями, имеющими структуру, подобную хлориду цезия, являются CsBr, CsI, высокотемпературный RbCl, AlCo, AgZn, BeCu, MgCe, RuAl и SrTl.

Структура каменной соли

октаэдрической геометрией

пространственная группа структуры каменной соли (NaCl) называется Fm3m (в нотации Германа – Могена ), или «225» (в Международных таблицах для кристаллографии). Обозначение Strukturbericht соответствует “B1”.

В структуре каменной соли или хлорида натрия (галита ) каждый из двух атомов Типы образуют отдельную гранецентрированную кубическую решетку, при этом две решетки взаимопроникают, образуя трехмерный узор в виде шахматной доски. С другой стороны, можно было бы рассматривать эту структуру как гранецентрированную кубическую структуру с вторичными атомами в ее октаэдрических отверстиях.

Примеры соединений с этой структурой включают сам хлорид натрия, наряду с почти всеми другими галогенидами щелочных металлов, и «многие оксиды, сульфиды, селениды и теллуриды двухвалентных металлов». В более общем смысле, эта структура с большей вероятностью будет образована, если катион несколько меньше, чем анион (отношение радиусов катион / анион от 0,414 до 0,732).

Координационное число каждого атома в этой структуре равно 6: каждый катион координирован с 6 анионами в вершинах октаэдра, и аналогично каждый анион координирован с 6 катионами в вершины октаэдра.

Межатомное расстояние (расстояние между катионом и анионом, или половина длины элементарной ячейки a) в некоторых кристаллах со структурой каменной соли составляет: 2,3 Å (2,3 × 10 м) для NaF, 2,8 Å для NaCl, и 3,2 Å для SnTe.

Другими соединениями, имеющими структуру, подобную каменной соли, являются LiF, LiCl, LiBr, LiI, NaF, NaBr, NaI, KF, KCl, KBr, KI, RbF, RbCl, RbBr, RbI, CsF, MgO, PbS, AgF, AgCl, AgBr и ScN.

Структура флюорита и антифлюоритовые структуры (AB 2) также являются структурами Fm3m, но имеют Соотношение ионов 1: 2. Они обозначены положениями Вайкоффа 4a и 8c, тогда как положения структур каменной соли – 4a и 4b.

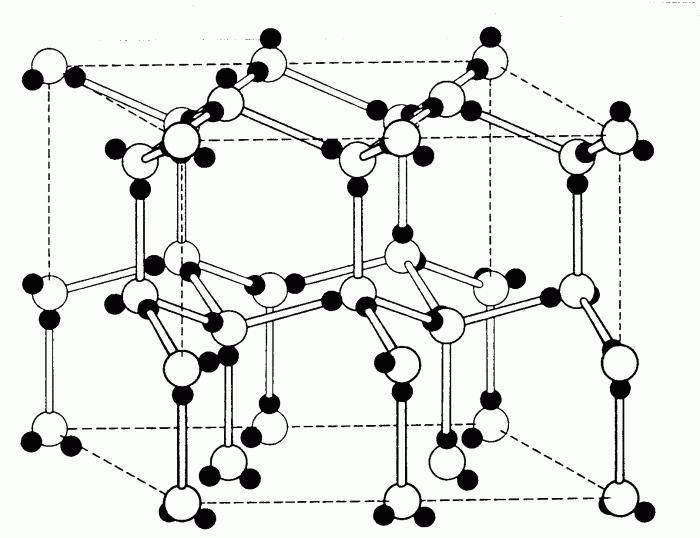
Структура цинковой обманки

Пространственная группа структуры цинковой обманки называется F43m (в нотации Германа – Могена ) или 216. Обозначение Strukturbericht – «B3».

Структура цинковой обманки (также обозначаемая как «цинковая обманка» “) назван в честь минеральной цинковой обманки (сфалерит ), одной из форм сульфида цинка (β-ZnS). Как и в структуре каменной соли, два типа атомов образуют две взаимопроникающие гранецентрированные кубические решетки. Однако он отличается от структуры каменной соли тем, как две решетки расположены относительно друг друга. Структура цинковой обманки имеет тетраэдрическую координацию : ближайшие соседи каждого атома состоят из четырех атомов противоположного типа, расположенных как четыре вершины . В целом расположение атомов в структуре цинковой обманки такое же, как в кубической структуре алмаза, но с чередующимися типами атомов в разных узлах решетки.

Примеры соединений с такой структурой включают саму цинковую обманку, нитрат свинца (II), многие сложные полупроводники (такие как арсенид галлия и теллурид кадмия ) и множество других бинарных соединений.

Другими соединениями, демонстрирующими структуру, подобную цинковой обманке, являются α-AgI, β-BN, алмаз, CuBr, β-CdS, BP и BAs.