Последовательное соединение пружин

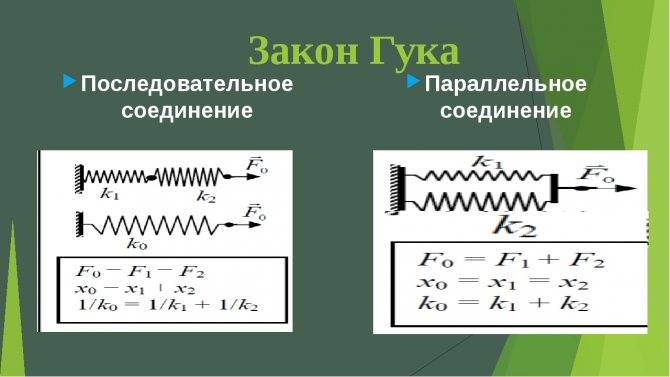
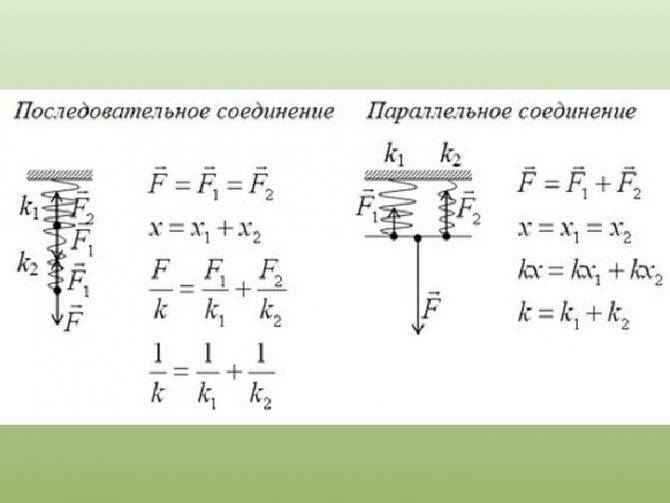
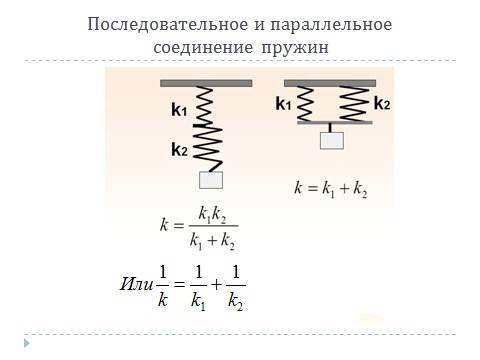
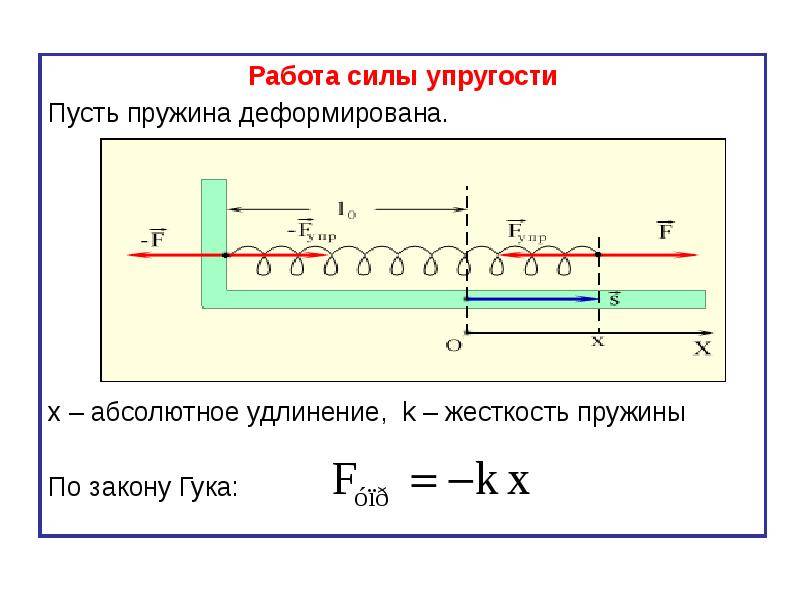
Опытный метод

Чтобы понять, как найти жесткость пружины, а точнее, определить коэффициент жесткости пружины опытным путем, следует произвести следующие манипуляции. Вам необходимо деформировать тело, прилагая к нему силу. Самый простой вид деформации – это сжатие или растяжение. Коэффициент жесткости показывает именно то, какую силу необходимо приложить к телу, чтобы упруго деформировать его на единицу длины. Мы сейчас говорим об упругой деформации, когда тело принимает свою первоначальную форму после совершения воздействия на него. Для того чтобы провести этот наглядный эксперимент вам потребуются следующие вещи:

• калькулятор,
• ручка,
• тетрадь,
• пружина,
• линейка,
• груз.

Итак, один конец пружины закрепите вертикально, а второй оставьте свободным. Измерьте длину пружины и запишите результат в тетрадь (это будет значение x1). Подвесьте к свободному концу пружины груз весом в сто граммов и опять измерьте длину пружины, запишите значение (x2). Рассчитайте абсолютное удлинение пружины (разница значений x1 и x2). При небольших сжатиях и растяжениях сила упругости пропорциональна деформации. Здесь уже применяем Закон Гука, согласно которому Fупр = |kx|, где k и является коэффициентом жесткости. Для того чтобы найти нужный нам коэффициент жесткости надо силу растяжения разделить на удлинение пружины. Силу растяжения находим следующим образом: Fупр = – N = -mg. Отсюда следует, что mg = kx. А значит, k = mg/x. Дальше все просто: подставьте известные вам значения в формулу и найдите, чему равна жёсткость пружины.

Определение

Силу, которая возникает в результате деформации тела и пытающаяся вернуть его в исходное состояние, называют силой упругости
.

Чаще всего ее обозначают ${\overline{F}}_{upr}$. Сила упругости появляется только при деформации тела и исчезает, если пропадает деформация. Если после снятия внешней нагрузки тело восстанавливает свои размеры и форму полностью, то такая деформация называется упругой.

Современник И. Ньютона Р. Гук установил зависимость силы упругости от величины деформации. Гук долго сомневался в справедливости своих выводов. В одной из своих книг он привел зашифрованную формулировку своего закона. Которая означала: «Ut tensio, sic vis» в переводе с латыни: каково растяжение, такова сила.

Рассмотрим пружину, на которую действует растягивающая сила ($\overline{F}$), которая направлена вертикально вниз (рис.1).

Силу $\overline{F\ }$ назовем деформирующей силой. От воздействия деформирующей силы длина пружины увеличивается. В результате в пружине появляется сила упругости (${\overline{F}}_u$), уравновешивающая силу $\overline{F\ }$. Если деформация является небольшой и упругой, то удлинение пружины ($\Delta l$) прямо пропорционально деформирующей силе:

\

где в коэффициент пропорциональности называется жесткостью пружины (коэффициентом упругости) $k$.

Жесткость (как свойство) – это характеристика упругих свойств тела, которое деформируют. Жесткость считают возможностью тела оказать противодействие внешней силе, способность сохранять свои геометрические параметры. Чем больше жесткость пружины, тем меньше она изменяет свою длину под воздействием заданной силы. Коэффициент жесткости – это основная характеристика жесткости (как свойства тела).

Коэффициент жесткости пружины зависит от материала, из которого сделана пружина и ее геометрических характеристик. Например, коэффициент жесткости витой цилиндрической пружины, которая намотана из проволоки круглого сечения, подвергаемая упругой деформации вдоль своей оси может быть вычислена как:

где $G$ – модуль сдвига (величина, зависящая от материала); $d$ – диаметр проволоки; $d_p$ – диаметр витка пружины; $n$ – количество витков пружины.

Единицей измерения коэффициента жесткости в Международной системе единиц (Си) является ньютон, деленный на метр:

\=\frac{\left}{\left}=\frac{Н}{м}.\]

Коэффициент жесткости равен величине силы, которую следует приложить к пружине для изменения ее длины на единицу расстояния.

Механизм образования поверхностного натяжения

В основе природы сил поверхностного натяжения лежит электростатическое притяжение молекул, находящихся на близком расстоянии в жидкости.

В самом деле, в жидкости, в отличие от газа, силы притяжения между молекулами больше, чем силы отталкивания, и энергия этого притяжения больше тепловой энергии, стремящейся распределить молекулы как можно шире. Поэтому равнодействующая сил, действующая на отдельную молекулу, будет направлена в сторону геометрического центра тела, образованного остальными молекулами.

В результате из-за отсутствия других сил молекулы жидкости всегда собираются в шарообразное тело. Равнодействующая сил, действующих на молекулы в глубине этого тела, практически равна нулю. Равнодействующая сил, действующая на молекулы на границе тела, направлена в сторону центра. Это приводит к тому, что плотность молекул внутри жидкости больше, чем плотность молекул, находящихся на границе. В результате в поверхностном слое возникают силы, стремящиеся к сокращению площади поверхности, — это и есть сила поверхностного натяжения.

Рис. 1. Силы, действующие на молекулы поверхности жидкости.

Расчет силы упругости

Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.

Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.

Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.

Разноцветная пластмассовая пружина-игрушка растяжению сопротивляется слабо

Закон Гука

Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал \( F_{\text{упр}} \) силой упругости.

\

Эту формулу назвали законом упругости Гука.

\( F_{\text{упр}} \left( H \right) \) – сила упругости;

\( \Delta L \left(\text{м} \right) \) – удлинение пружины;

\( \displaystyle k \left(\frac{H}{\text{м}} \right) \) – коэффициент жесткости (упругости).

Какие деформации называют малыми

Закон Гука применяют для малых удлинений (деформаций).

Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.

Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.

Как рассчитать коэффициент жесткости

Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.

Рис. 4. Вес подвешенного на пружине груза уравновешивается силой упругости

Так как силы взаимно компенсируются, в правой части уравнения находится ноль.

\

Подставим в это уравнение выражение для силы упругости

\

Прибавим к обеим частям вес груза и разделим на измеренное изменение длины \(\Delta L \) пружины. Получим выражение для коэффициента жесткости:

\

\(g\) – ускорение свободного падения, оно связано с силой тяжести.

Сила Архимеда

Сила возникает в результате взаимодействия тела с жидкость (газом), при его погружении в жидкость (или газ). Эта сила выталкивает тело из воды (газа). Поэтому направлена вертикально вверх (выталкивает). Определяется по формуле:

В воздухе силой Архимеда пренебрегаем.

Если сила Архимеда равна силе тяжести, тело плавает. Если сила Архимеда больше, то оно поднимается на поверхность жидкости, если меньше – тонет.

Существуют силы электрического происхождения. Возникают при наличии электрического заряда. Эти силы, такие как Сила Кулона, сила Ампера, сила Лоренца.

I закон Ньютона

Существуют такие системы отсчета, которые называются инерциальными, относительно которых тела сохраняют свою скорость неизменной, если на них не действуют другие тела или действие других сил скомпенсированно.

II закон Ньютона

Ускорение тела прямопропорционально равнодействующей сил, приложенных к телу, и обратно пропорционально его массе:

III закон Ньютона

Силы, с которыми два тела действуют друг на друга, равны по модулю и противоположны по направлению.

Локальная система отсчёта

— это система отсчёта, которая может считаться инерциальной, но лишь в бесконечно малой окрестности какой-то одной точки пространства-времени, или лишь вдоль какой-то одной незамкнутой мировой линии.

Преобразования Галилея. Принцип относительности в классической механике.

Преобразования Галилея. Рассмотрим две системы отсчета движущиеся друг относительно друга и с постоянной скоростью v.Одну из этих систем обозначим буквой K. Будем считать неподвижной. Тогда вторая система Kбудет двигаться прямолинейно и равномерно. Выберем координатные оси x,y,z системы K и x’,y’,z’ системы K’ так что оси x и x’ совпадали, а оси y и y’ , z и z’, были параллельны друг другу. Найдем связь между координатами x,y,z некоторой точки P в системе K и координатами x’,y’,z’ той же точки в системе K’. Если начать отсчёт времени с того момента, когда начало координат системы, совпадали, то x=x’+v, кроме того, очевидно, что y=y’, z=z’. Добавим к этим соотношениям принятое в классической механике предположение, что время в обеих системах течёт одинаковым образом, то есть t=t’. Получим совокупность четырёх уравнений : x=x’+vt;y=y’;z=z’;t=t’, названных преобразованиями Галилея.Механический принцип относительности.Положение о том, что все механические явления в различных инерциальных системах отсчёта протекают одинаковым образом, вследствие чего никакими механическими опытами невозможно установить, покоится ли система или движется равномерно и прямолинейно носит названия принцип относительности Галилея.Нарушение классического закона сложения скоростей.Исходя из общего принципа относительности (никаким физическим опытом нельзя отличить одну инерциальною систему от другой), сформулированным Альбертом Эйнштейном, Лоуренс изменил преобразования Галилиея и получил : x’=(x-vt)/(1-v 2 /c 2 ); y’=y; z’=z; t’=(t-vx/c 2 )/(1-v 2 /c 2 ). Эти преобразования называются преобразованиями Лоуренса.

Пружины можно назвать одной из наиболее распространенных деталей, которые являются частью простых и сложных механизмов. При ее изготовлении применяется специальная проволока, накручиваемая по определенной траектории. Выделяют довольно большое количество различных параметров, характеризующих это изделие. Наиболее важным можно назвать коэффициент жесткости. Он определяет основные свойства детали, может рассчитываться и применяться в других расчетах. Рассмотрим особенности подобного параметра подробнее.

Видео

Из этого видео вы узнаете, как определить жесткость пружины.

Чем большей деформации подвергается тело, тем значительней в нем возникает сила упругости. Это значит, что деформация и сила упругости взаимосвязаны, и по изменению одной величины можно судить об изменении другой. Так, зная деформацию тела, можно вычислить возникающую в нем силу упругости. Или, зная силу упругости, определить степень деформации тела.

Если к пружине подвешивать разное количество гирек одинаковой массы, то чем больше их будет подвешено, тем сильнее пружина растянется, то есть деформируется. Чем больше растянута пружина, тем большая в ней возникает силы упругости. Причем опыт показывает, что каждая следующая подвешенная гирька увеличивает длину пружины на одну и туже величину.

Так, например, если исходная длина пружины была 5 см, а подвешивание на ней одной гирьки увеличило ее на 1 см (т. е. пружина стала длиной 6 см), то подвешивание двух гирек увеличит ее на 2 см (общая длина составит 7 см), а трех — на 3 см (длина пружины будет 8 см).

Еще до опыта известно, что вес и возникающая под его действием сила упругости находятся друг с другом в прямопропорциональной зависимости. Кратное увеличение веса во столько же раз увеличит силу упругости. Опыт же показывает, что деформация точно также зависит от веса: кратное увеличение веса во столько же раз увеличивает изменения в длине. Это значит, что, исключив вес, можно установить прямопропорциональную зависимость между силой упругости и деформацией.

Если обозначить удлинение пружины в результате ее растяжения как x или как ∆ l ( l ₁ – l , где l — начальная длина, l ₁ — длина растянутой пружины), то зависимость силы упругости от растяжения можно выразить такой формулой:

В формуле используется коэффициент k . Он показывает, в какой именно зависимости находятся сила упругости и удлинение. Ведь удлинение на каждый сантиметр может увеличивать силу упругости одной пружины на 0,5 Н, второй на 1 Н, а третьей на 2 Н. Для первой пружины формула будет выглядеть как F_упр = 0,5x, для второй — F_упр = x, для третьей — F_упр = 2x.

Коэффициент k называют жесткостью пружины. Чем жестче пружина, тем труднее ее растянуть, и тем большее значение будет иметь k. А чем больше k, тем больше будет сила упругости (F_упр) при равных удлинения (x) разных пружин.

Жесткость зависит от материала, из которого изготовлена пружина, ее формы и размеров.

Единицей измерения жесткости является Н/м (ньютон на метр). Жесткость показывает, сколько ньютонов (сколько сил) надо приложить к пружине, чтобы растянуть ее на 1 м. Или насколько метров растянется пружина, если приложить для ее растяжения силу в 1 Н. Например, к пружине приложили силу в 1 Н, и она растянулась на 1 см (0,01 м). Это значит, что ее жесткость равна 1 Н / 0,01 м = 100 Н/м.

Также, если обратить внимание на единицы измерения, то станет понятно, почему жесткость измеряется в Н/м. Сила упругости, как и любая сила, измеряется в ньютонах, а расстояние – в метрах

Чтобы уровнять по единицам измерения левую и правую части уравнения Fупр = kx, надо в правой части сократить метры (то есть поделить на них) и добавить ньютоны (то есть умножить на них)

Чтобы уровнять по единицам измерения левую и правую части уравнения Fупр = kx, надо в правой части сократить метры (то есть поделить на них) и добавить ньютоны (то есть умножить на них).

Соотношение между силой упругости и деформацией упругого тела, описываемое формулой F_упр = kx, открыл английский ученый Роберт Гук в 1660 году, поэтому это соотношение носит его имя и называется законом Гука.

Упругой деформацией является такая, когда после прекращения действия сил, тело возвращается в свое исходное состояние. Бывают тела, которые почти нельзя подвергнуть упругой деформации, а у других она может быть достаточно большой. Например, поставив тяжелый предмет на кусок мягкой глины, вы измените его форму, и этот кусок сам уже не вернется в исходное состояние. Однако если вы растяните резиновый жгут, то после того, как отпустите его, он вернет свои исходные размеры. Следует помнить, что закон Гука применим только для упругих деформаций.

Формула F_упр = kx дает возможность по известным двум величинам вычислять третью. Так, зная приложенную силу и удлинение, можно узнать жесткость тела. Зная, жесткость и удлинение, найти силу упругости. А зная силу упругости и жесткость, вычислить изменение длины.

Принципы деформации

Когда сила воздействует на материал, он растягивается или сжимается в ответ. В механике сила, приложенная на единицу площади, является тем, что называется напряжением. Степень растяжения и сжатия, возникающая, когда материал реагирует на напряжение, называется деформацией. Напряжение измеряется отношением разницы в длине к исходной длине в направлении напряжения.

Каждый материал по-разному реагирует на стресс, и детали этой реакции важны для инженеров, выбирающих материалы для своих конструкций и машин, которые должны вести себя предсказуемо при ожидаемых напряжениях.

Для большинства материалов нагрузка, испытываемая при приложении небольшого напряжения, зависит от плотности химических связей. То же самое относится к жёсткости материала, которая напрямую связана с его химической структурой.

Происходящее при снятии напряжения зависит от того, насколько далеко перемещены атомы.

В целом существует два типа деформации:

1. Упругая. После снятия напряжения материал возвращается к размеру, который был до приложения нагрузки. Деформация обратима, непостоянна.
2. Пластическая. Напряжение настолько велико, что при снятии нагрузки материал не возвращается к своему предыдущему размеру. Минимальное значение напряжения, вызывающего пластическую деформацию, известно как предел упругости материала.

Как определить жесткость воды

Очень сложно определить на ощупь, какая вода — жесткая или мягкая. Термин «жёсткость» возник потому, что после стирки ткани теряют мягкость, шерстистость или шелковистость, становятся неприятно жесткими на ощупь. Ткацкие или трикотажные переплетения, независимо от плотности, имеют пористую структуру. К волокнам присоединяются соли, что делает вещи после стирки более грубыми, жесткими, плотными.

Определить жесткость воды в можно как в лаборатории, так и в домашних условиях. Наличие солей жесткости можно определить визуально:

• Напитки имеют неприятный горчащий вкус.
• Чаи завариваются дольше обычного.
• Мясо при варке становится неприятно жестким.
• На стенках посуды заметны солевые отложения.
• На приборах образуется обильная накипь.
• На волосах после мытья и на расческе остается белесый налет.
• Мыло и порошок плохо пенятся, при стирке увеличивается их расход.

Повышенная жесткость питьевой воды может причинить ущерб здоровью и нагревательным приборам. Не зная точных показателей концентрации солей, сложно рассчитать дозу средств от накипи для стирально-сушильных агрегатов или запрограммировать на чистку кофемашину. Трудно обеспечить комфортное обитание рыбкам в аквариуме или правильно выбрать фильтры очистки. Помимо визуальной оценки лучше использовать более точные измерительные методы определения жесткости питьевой и технической воды.

Измерение жесткости воды

Перед употреблением в пищу, перед поливом огорода, перед подачей в трубопроводы или перед техническим применением воды для производственных процессов полезно проверить наличие солей жесткости. Такая проверка снимет претензии потребителей к водоснабжающим компаниям, продлит срок службы дорогого промышленного оборудования.

Для измерения жесткости воды используют бытовые и профессиональные приборы:

1. Медицинские полоски, продающиеся в аптеках, выдают хороший результат с точностью до 1-2°Ж.
2. Экспресс-тесты для аквариума позволяют следить за подачей воды в емкости с водными обитателями или проверять растворы, предназначенные для полива растений.
3. Солемер, спектроанализатор, TDS и EC-метр показывают содержание солей и иные параметры: удельную электропроводность, сопротивление раствора.

Полезно заказать исследование в лаборатории, чтобы получить точные результаты с подтверждающей документацией. Тогда не придется думать, чем определить жесткость воды, не нужно покупать измерительные приборы или рассчитывать показатели по косвенным параметрам, используя формулы.

Как определить жесткость воды по формуле

Определить жесткость воды можно по формуле. Для определения общих показателей нужно выполнить расчет:

Жо = + = (m(Ca2+))/(Э(Ca2+) x V(H2O)) + (m(Mg2+))/(Э(Mg2+) x V(H2O)),

где:

; — концентрация ионов кальция и магния, в мг-экв/дм3;

m(Ca2+); m(Mg2+) — содержание ионов в мг;

V(H2O) — объем воды, дм3;

Э -эквивалентная масса ионов* (её значения уже приводились в тексте: Ca2+=20,04; Mg2+=12,16 мг/лили г/моль).

Расчетный результат получается в единицах: мг-экв/дм3.

Далее вычисляют временную или постоянную жёсткость. Рассчитанную величину вычитают из Жо и получают значения всех трёх категорий Ж.

Карбонатная Жк вычисляется по формуле:

Жк = = (m(HCO3))/(Э(HCO3) х V(H2O))

Некарбонатная: Жнк=Жо-Жк.

Физика

3.4. Механическая энергия

3.4.2. Потенциальная энергия

Потенциальная энергия — это механическая энергия системы тел, определяемая их (или частей одного тела) взаимным расположением.

Потенциальная энергия деформированной пружины

Деформированная пружина (сжатая или растянутая) (рис. 3.7) обладает потенци­альной энергией, которая определяется формулой

W p = k ( Δ l ) 2 2 ,

где k — коэффициент жесткости (упругости) пружины; ∆l — величина абсолютной деформации пружины (удлинения или сжатия).

Рис. 3.7

Потенциальная энергия недеформированной пружины равна нулю.

Следует отметить, что потенциальная энергия деформированной пружины всегда является положительной величиной.

В Международной системе единиц потенциальная энергия деформированной пружины измеряется в джоулях (1 Дж).

Потенциальная энергия взаимодействия тела и Земли

Тело, расположенное на расстоянии h над поверхностью Земли (или под ее поверхностью), обладает потенциальной энергией, которая определяется формулой

Wp = mgh + C,

где m — масса тела; g — модуль ускорения свободного падения.

Выбор константы C является условным и зависит от конкретной задачи; часто указанную константу выбирают таким образом, чтобы на поверхности планеты потенциальная энергия взаимодействия тела и планеты обращалась в ноль.

Следует отметить, что потенциальная энергия взаимодействия тела и Земли может быть как положительной, так и отрицательной величиной.

В Международной системе единиц потенциальная энергия тела, поднятого на некоторую высоту относительно поверхности Земли, измеряется в джоулях (1 Дж).

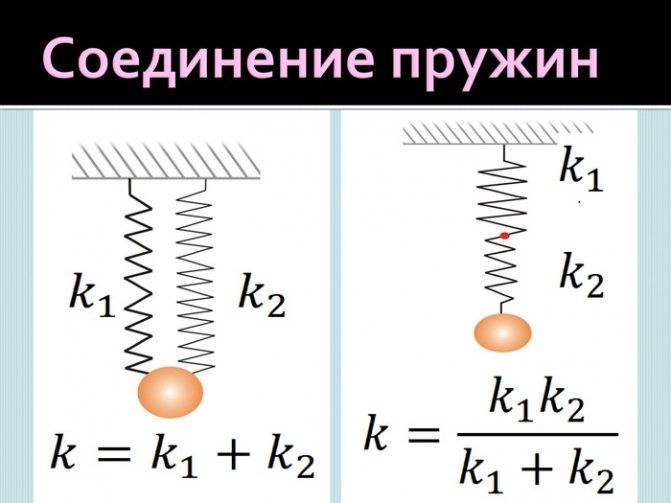
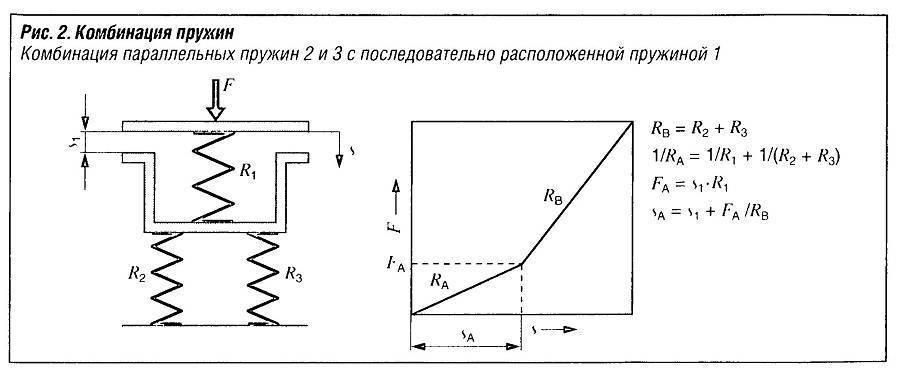
Пример 26. Две пружины с одинаковыми коэффициентами жесткости по 1,0 кН/м соединили последовательно. Составную пружину растянули на 10 см. Во сколько раз увеличится потенциальная энергия деформации, если эти же пружины соединить параллельно, а величину деформации системы оставить прежней? Рассчитать потенциальную энергию пружин при последовательном и параллельном соединении, считая деформацию составной пружины одинаковой и равной 10 см.

Решение. Потенциальная энергия составной пружины определяется формулой

W p = k общ ( Δ l ) 2 2 ,

где kобщ — общий коэффициент жесткости составной пружины; ∆l — величина деформации пружины.

Коэффициент жесткости составной пружины определяется по-разному:

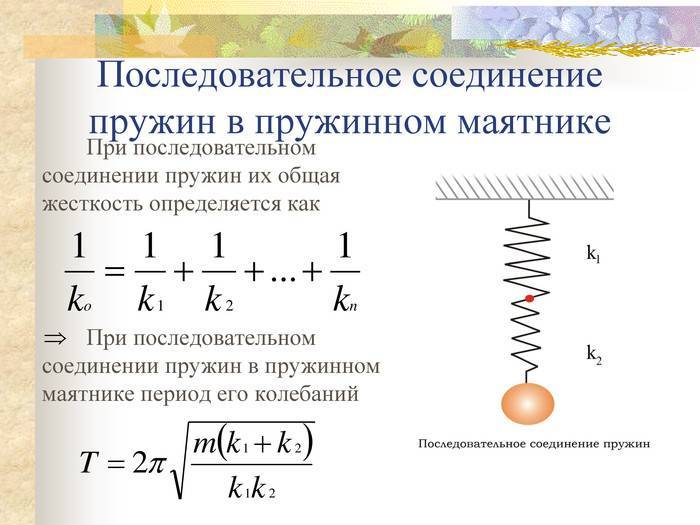
для N одинаковых пружин, соединенных последовательно,

k общ 1 = k 0 N ;

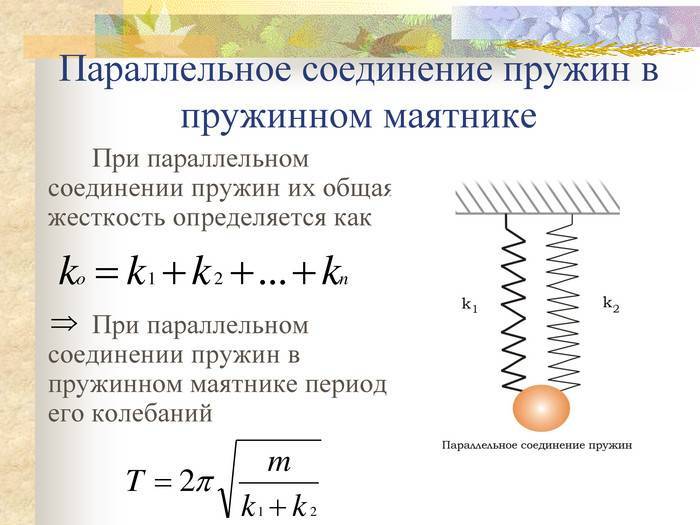
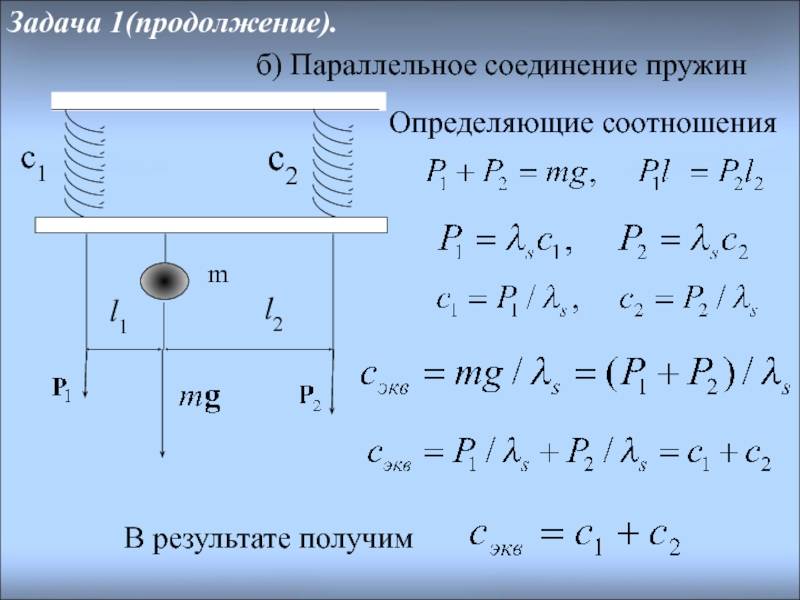
для N одинаковых пружин, соединенных параллельно,

kобщ2 = Nk0,

где k0 — коэффициент жесткости одной пружины; N = 2 — количество соединенных пружин.

Потенциальная энергия составной пружины вычисляется по формулам:

для N одинаковых пружин, соединенных последовательно,

W p 1 = k общ 1 ( Δ l ) 2 2 = k 0 ( Δ l ) 2 2 N ;

для N одинаковых пружин, соединенных параллельно,

W p 2 = k общ 2 ( Δ l ) 2 2 = N k 0 ( Δ l ) 2 2 .

Отношение потенциальных энергий

W p 1 W p 2 = k 0 ( Δ l ) 2 2 N 2 N k 0 ( Δ l ) 2 = 1 N 2

определяется только количеством пружин и не зависит от деформации составной пружины.

Рассчитаем потенциальную энергию составной пружины, состоящей из двух одинаковых пружин,

соединенных последовательно:

W p 1 = k 0 ( Δ l ) 2 2 N = 1,0 ⋅ 10 3 ( 10 ⋅ 10 − 2 ) 2 2 ⋅ 2 = 2,5 Дж;

соединенных параллельно:

W p 2 = N k 0 ( Δ l ) 2 2 = 2 ⋅ 1,0 ⋅ 10 3 ( 10 ⋅ 10 − 2 ) 2 2 = 10 Дж.

Отношение указанных потенциальных энергий равно

W p 1 W p 2 = 1 N 2 = 1 2 2 = 4 .

Следовательно, при одинаковой деформации потенциальная энергия пружины, составленной из двух одинаковых параллельно соединенных пружин, в 4 раза больше потенциальной энергии пружины, составленной из двух одинаковых последовательно соединенных пружин.

Пример 27. Какой энергией обладает тело массой 500 г на вершине горы относительно дна озера, находящегося у подножия горы? Высота горы составляет 1,50 км, а глубина озера 250 м.

Решение. Потенциальная энергия тела, поднятого на некоторую высоту, определяется формулой

Wp = mgh,

где m — масса тела; g — модуль ускорения свободного падения; h — высота, на которую поднято тело над определенным уровнем, характеризуемым нулевым значением потенциальной энергии.

Выберем нулевой уровень потенциальной энергии (Wp = 0) на дне озера так, как показано на рисунке.

Тогда высота, на которую поднято тело над указанным уровнем, является суммой:

h = h2 + h2,

где h2 = 1,50 км — высота горы; h2 = 250 м — глубина озера.

Потенциальная энергия тела относительно дна озера определяется выражением

Wp = mg(h2 + h2).

Расчет дает значение:

W p = 500 ⋅ 10 − 3 ⋅ 10 ⋅ ( 1,50 + 0,25 ) ⋅ 10 3 = 8,75 ⋅ 10 3 Дж = 8,75 кДж.

Видео

Из этого видео вы узнаете, как определить жесткость пружины.

Суть метода заключается в том, что пружину нагружают силой определенной величины (в нашем случае, вес груза)

.

Дожидаются наступления статического равновесия пружины и замеряют ее деформацию под воздействием этой силы

.

Величина коэффициента жесткости

Далее определяются максимальное ( ) и минимальное ( ) значения коэффициента жесткости по следующим принципам

, (12)

, (13)

где , , , , , – максимальные и минимальные значения величин, задействованных в формулах.

Затем, поскольку коэффициент жесткости распределяется по симметричному «нормальному закону», по формулам, приведенным ниже для величин, определяются среднее значение коэффициента жесткости, половина доверительного интервала и относительная погрешность результата

(14)

(15)

. (16)

Определение коэффициента жесткости пружины методом строительной механики

Коэффициент жесткости определяется по зависимости

. (17)

С использованием формулы 17, а также зависимостей 12 и 13 определяются максимальное ( ) и минимальное ( ) значения коэффициента жесткости.

Затем, по формулам 14, 15 и 16 определяются среднее значение коэффициента жесткости, половина доверительного интервала и относительная погрешность результата.

ИТОГИ ЛАБОРАТОРНОЙ РАБОТЫ И ОФОРМЛЕНИЕ ОТЧЕТА

Итоги лабораторной работы

Анализируя полученные результаты необходимо сравнить методы определения коэффициента жесткости по критериям точности и сложности. Далее, дать оценку точности и достоверности полученных результатов, а также предложить меры по повышению точности результатов в случае неудовлетворительности последних.

Оформление отчета

Оформляется один отчет на бригаду на листах формата А4.

В отчете должны быть приведены все необходимые данные, расчеты и пояснения, результаты и выводы.

Отчет должен содержать следующие обязательные элементы: титульный лист с фамилиями выполнявших работу и проверяющего, оглавление с указанием номеров страниц начала разделов, нумерацию страниц, и разделы в следующем порядке:

1) исходные данные (см. п. 2.3),

2) определение статистических оценок измеренных величин,

3) определение коэффициента жесткости пружины статическим методом,

4) определение коэффициента жесткости пружины методом строительной механики,

Все появляющиеся первый раз переменные должны быть сопровождены пояснениями. Например,

деформация пружины – или

или

–модуль упругости стали при сдвиге.

У всех значений величин, имеющих размерность, должны стоять соответствующие единицы измерения. Все формулы должны быть раскрыты и сосчитаны. Например,

=176-138=38 мм.

Все рисунки и таблицы должны иметь названия и сквозную нумерацию.

СПИСОК ЛИТЕРАТУРЫ

1. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1962. – 576 с.

2. ГОСТ 24026-80 Исследовательские испытания. Планирование эксперимента. Термины и определения.

3. Налимов В. В. Теория эксперимента – М.: Наука, 1971. – 207 с.

4. Румшиский Л.3. Математическая обработка результатов эксперимента – М.: Главная редакция физико-математической литературы изд-ва «Наука», 1971. – 192 с.

Приложение

	0.9	0.95	0.98	0.99	0.999
2.132	2.776	3.747	4.604	8.610
2.015	2.571	3.365	4.032	6.859
1.943	2.447	3.143	3.707	5.959
1.895	2.365	2.998	3.499	5.405
1.860	2.306	2.896	3.355	5.041
1.833	2.262	2.821	3.250	4.781
1.812	2.228	2.764	3.169	4.587
1.796	2.201	2.718	3.106	4.487
1.782	2.179	2.681	3.055	4.318
1.771	2.160	2.650	3.012	4.221
1.761	2.145	2.624	2.977	4.140
1.753	2.131	2.602	2.947	4.073
1.746	2.120	2.583	2.921	4.015
1.734	2.103	2.552	2.878	3.922
1.725	2.086	2.528	2.845	3.850
1.708	2.060	2.485	2.787	3.725
1.697	2.042	2.457	2.750	3.646
1.689	2.030	2.437	2.724	3.591
1.684	2.021	2.423	2.704	3.551
1.679	2.014	2.412	2.689	3.522
1.676	2.008	2.403	2.677	3.497
1.671	2.000	2.390	2.660	3.460
1.667	1.995	2.381	2.648	3.436
1.664	1.990	2.374	3.639	3.416
1.662	1.987	2.368	2.632	3.401
1.660	1.984	2.364	2.626	3.391
	1.645	1.960	2.326	2.576	3.291

Учебно-методическое пособие по выполнению расчетных работ

Одерышев Андрей Васильевич

ОСНОВЫ НАУЧНЫХ ИССЛЕДОВАНИЙ

Печатается в авторской редакции

Подписано в печать Сдано в производство

Формат 1/16 Усл.-печ. л. Уч.-изд. л. 2.

Тираж 100 экз. Заказ №

Государственный университет морского и речного флота им. адм. С.О. Макарова,

198035, Санкт-Петербург, улица Двинская, 5/7

Отпечатали в типографии ФБОУ ВПО ГУМРФ

198035, Санкт – Петербург, Межевой канал, 2

Основные разновидности

Широкое распространение получили четыре вида пружин, которые устанавливаются на все современные автомобили.

1. Стандартные. Их можно считать базовым вариантом, который устанавливается в заводских условиях при изготовлении автомобиля. Такие элементы рассчитаны на эксплуатацию ТС в стандартных условиях, регламентированных техническим паспортом авто.
2. Усиленные. Предназначены для улучшения эксплуатационных характеристик ТС, которое используется в условиях бездорожья, при постоянных перевозках груза или буксировке прицепов.
3. Завышающие. После установки способствуют повышению дорожного просвета и грузоподъемности автомобиля.
4. Занижающие. В основном, такие образцы устанавливают любители спортивной езды, поскольку занижают клиренс и смещают центр тяжести автомобиля книзу.

О том, для чего нужны автомобилю пружины и как не ошибиться с выбором, можно посмотреть на видео: https://www.youtube.com/watch?v=OflrYHXtirI .